6 Null Hypothesis Significant Testing

Null hypothesis significance testing (NHST) is a controversial approach to testing hypotheses. It is a commonly-used approach in psychological science.

Simply, NHST begins with an assumption, a hypothesis, about some effect in a population. Data is collected that is believed to be representative of that population (see previous chapter on Samples and Populations). Should the data not align with the null hypothesis, it is taken as evidence against it.

There are several concepts related to NHST and its misconceptions that need to be addressed to facilitate your understanding and research.

6.1 p-values

Prior to exploring p-values, let’s ensure you have a basic understanding of probability notation. I recommend you review the chapter on probability first. Back to the notation…:

$p (x)$ which would indicate the probability of $x$ .

For example, the probability of flipping a coin and getting a heads, $p (h e a d s) = .5$ . This indicates a 50% probability of getting a heads. Probability ranges from 0 (no chance), to 1 (guarantee). For example, the probability that you, the person reading this, is a Grenfell student is high. Thus, my best guess right now is that $p (3950 s t u d e n t) = .95$ . Hypothetically, if I could survey everyone who has read this sentence, I would expect 19 out of 20 of them to be a Grenfell student. I would expect one of them not to be (e.g., someone randomly stumbled on this page…lucky you!).

Additionally, I could use the notation for a conditional probability:

$p (x | y)$ which would indicate the probability of $x$ , given $y$ .

For example, what if I provided more details in the previous coin-flipping example? The coin is not a fair coin. Well, the original probability will only be our best guess if the coin is fair. That is, p(heads|fair coin) = .5. However, with the new information, p(heads|unfair coin) $\neq$ .5. Perhaps our coin is biased to land on heads more often than tails. Thus, we would expect that $p (h e a d s) > .5$ .

The reverse of a conditional probability is not always equal to the original conditional probability. That is, $p (x | y) \neq p (y | x)$ . Consider the following: what is the probability that someone is Canadian, given that they are the prime minister of Canada: p(Canadian|Prime Minister)? While not legally required, it is quite likely that if someone is the prime minister of Canada, they are Canadian.

Do you think this is equal to the probability that someone is the Prime Minister of Canada, given that they are Canadian: p(Prime Minister|Canadian)? I would argue that the former is $p = 1.00$ , while the later is not. In fact, the later can be calculated. Given there are about $38, 000, 000$ Canadians, and there is only one current Prime Minister, than the probability that someone is Prime Minister, given that they are Canadian p(Prime Minister|Canadian)= $\frac{1}{38, 000, 000}$ =.0000000263. So:

p(Canadian|Prime Minister) = 1.00
p(Prime Minister|Canadian)=.0000000263

It is imperative understand conditional probability and that the reverse conditional probability likely differs from the initial.

A key feature of NHST is that the null hypothesis is assumed to be true. Given this assumption, we can estimate how likely a set of data are. This is what a p-value tells you.

The p-value is the probability of obtaining data as or more extreme than you did, given a true null hypothesis. We can use our notation:

$p (D | H_{0})$

Where D is our data (or more extreme) and $H_{0}$ is the null hypothesis.

When the p-value meets some predetermined threshold, it is often referred to as statistical significance. This threshold has typically, and arbitrarily been $α = .05$ . Should data be so unlikely that is crosses the threshold (i.e., $p < .05$ ), we take it as evidence against the null hypothesis and reject it. If it is below the threshold ( $p > .05$ ), we fail to reject it. Note: we do not accept the null hypothesis. Liken this to a courtroom verdict, which is that someone is guilty or not guilty. A not guilty verdict does not mean that someone is innocent, it means there is not enough evidence to convict.

…beginning with the assumption that the true effect is zero (i.e., the null hypothesis is true), a p-value indicates the proportion of test statistics, computed from hypothetical random samples, that are as extreme, or more extreme, then the test statistic observed in the current study.

(Spence & Stanley, 2018)

or, stated another way:

The smaller the p-value, the greater the statistical incompatibility of the data with the null hypothesis, if the underlying assumptions used to calculate the p-value hold. This incompatibility can be interpreted as casting doubt on or providing evidence against the null hypothesis or the underlying assumptions.

(Wesserstein & Lazar, 2016)

Simply, a p-values indicates the probability of your, or more extreme, test statistic, assuming the null: $p (d a t a | n u l l)$ . For ease, consider the following table:

		Reality
		No Effect ( $H_{o}$ True)	Effect ( $H_{1}$ True)
Research Result	No Effect ( $H_{o}$ True)	Correctly Fail to Reject $H_{o}$	Type II Error ( $β$ )
	Effect ( $H_{1}$ True)	Type I Error ( $α$ )	Correctly Reject $H_{o}$

When we conduct NHST, we are assuming that the null hypothesis is indeed true, despite never truly knowing this. As noted, a p-value indicates the likelihood of your or more extreme data given the null.

6.1.1 If the null hypothesis is true, why would our data be extreme?

In inferential statistics we make inferences about population-level parameters based on sample-level statistics. For example, we infer that a sample mean is indicative of and our best estimate of a population mean.

In, NHST, we assume that population-level effects or associations (i.e., correlations, mean differences, etc.) are zero, null, nothing at a population level (note: this is not always the case). If we sampled from a population whose true effect or association was $0$ an infinite number of times, we would not always get a sample statistic of 0 (i.e., our true null effect) because of random variations in our sample and our sampling. Instead, our sample statistics would form a distribution around the population parameter. Consider a population correlation of $ρ = 0$ .

p versus

ρ

A p-value is a probability value. It is an italicized p. Specifically, the probability of obtaining your or more extreme data given a true null hypothesis.

$ρ$ is the greek symbol ‘rho’, a blend of the letters r and o (pronounced row). It is used to represent a population parameter for a correlation.

While $ρ$ represents the population correlation, $r$ represents a sample correlation.

If we took 10,000 samples of size $n$ from this population with $ρ = 0$ , let’s say 20 people, we would get a distribution that looks something like:

The above shows the distribution of 10,000 correlation coefficients derived from simulated samples from a population that has $ρ = 0$ (i.e., the true population correlation is 0). Although not quite an infinite number of samples, I hope you get the idea that the sample statistics form a normal distribution around the true population parameter. The red shaded region shows the two tails of this distribution that encompass the most extreme 5% of the samples (2.5% per tail). That is, 5% of the samples are in the tails (2.5% in each tail). These extreme 5% fall at about a correlation of $r \geq .444$ or $r \leq - .444$ . Thus, there is a low probability of getting a correlation beyond $+ / - .444$ when the null hypothesis is true. Only 5% of the samples are at or beyond this number.

While we used simulated data from a hypothesized population, math people have derived formulas that represent the approximate shape of the curve for infinite samples. We don’t need to know the calculus behind it, but the curve for a null population correlation ( $ρ = 0$ ) and a sample size of 20 would approximate:

In the above, the extreme 5% of the curve is associated with a correlation of $r = | .44377 |$ ; that is, the extreme 2.5% of samples have correlations that are larger higher than $r = | .44377 |$ or 2.5% have correlations lower than $r = - .44377$ . Let’s us run a correlation on one of these samples. The following is the data for two variables, $x$ and $y$ .

Participant	x	y
1	-1.4759696	-0.9109435
2	0.5658273	-1.8701988
3	0.1805740	0.2642193
4	-0.6255420	1.9641472
5	-0.4936539	-0.6887534
6	1.6158737	1.4952663
7	-0.7168520	-0.4804542
8	0.4519491	0.4608354
9	-0.2398118	0.1772640
10	0.8316019	0.4042273
11	-0.6183224	-0.7441028
12	-0.5682177	-0.3891823
13	0.7711289	0.5722868
14	-2.6018589	-1.3421923
15	-0.5064533	-1.0413429
16	-0.0043281	1.5822809
17	1.3737851	0.6665896
18	0.9755060	-0.6206455
19	0.5090296	0.1514108
20	0.5757341	0.3492881

The following are the results of a correlation test on this data.

Correlation Coefficient	p-value
0.444	0.05

These results suggest the correlation in the sample is $r = .444$ and $p = .05$ . What does this mean? How would you interpret this p-value? Try to link it to the distribution of samples from above.

Think about it

The p-value indicates that given a true null hypothesis, we would expect a correlation coefficient as big or bigger than ours only 5% of the time.

In the distribution of sample test statistics above, this aligns with the fact that 5% of the statistics (2.5% in each tail) were at least $r = | .444 |$ .

Because the probability of this data is quite low (i.e., we obtained an extreme statistic), given $H_{0}$ , we often reject the null hypothesis. Our data is very unlikely given a true null hypothesis, therefore we reject the null.

6.1.2 Why is $α = .05$

You have often looked for “ $p < .05$ ” to map onto your a priori alpha level ( $α = .05$ ). Why though? The magnitude of the tails is arbitrary, for the most part, but has been set to a standard of 5% (corresponding $α = .05$ ) since the early 20th century, which is a further criticism of NHST. However, we set our $α$ threshold/criteria, and as demonstrated in the previous paragraph, our $α$ level influences the correlation coefficient we would consider statistically significant. Imagine we wanted to reduce out criteria, such that $α = .01$ . What do you think would happen to the red shaded region in the above graphs and the critical correlation coefficient? If we wanted to adjust what we consider extreme so that it is less conservative, which is essentially what we are doing when we reduce our alpha, we would shift the red regions outward and our critical correlation coefficients would be larger in absolute magnitude. In this case, our graph would be:

The yellow region represents the extreme 1% of the distribution (0.5% per tail). The red region is where the original regions were for $α = .05$ .The proportion of samples in the red region is? You guessed it, 4%. These 4% of samples have correlations, $.561 > r \geq .444$ . Remember, these are for a sample of $n = 20$ . The critical correlation coefficients differ based on sample size because they influence the standard errors (i.e., it gets skinnier or fatter).

So, we set the criterion of $α$ a priori and our resultant p-value lets us decide if our data are probable (or not) given $H_{0}$ . If it’s lower than our criterion we can reject $H_{0}$ , suggesting only that the population effect is not zero. It is often called statistically significant. Otherwise, if our p-value is larger than our criterion, we decide that our data is not that unlikely and fail to reject that $H_{0}$ . Here, it’s plausible that the true population parameter is 0 (but not confirming that the parameter is 0).

In short, p-values are the probability of getting a set of data or more extreme given the null. We compare this to a criterion cut-off, $α$ . If our data is very improbable given the null, so much that is is less than our proposed cutoff, we say it is statistically significant.

6.1.3 Misconceptions

Many of these misconceptions have been described in detail elsewhere (e.g., Nickerson, 2000). I visit only some of them.

6.1.3.1 1. Odds against chance fallacy

The odds against chance fallacy suggests that a p-value indicates the probability that the null hypothesis is true. For example, someone might conclude that if their $p = .04$ , there is a 4% chance that the null hypothesis is true. You have learned that p-values indicate $p (D | H_{0})$ and that you cannot simply flip the conditional probabilities: $p (D | H_{0}) \neq p (H_{0} | D)$ . The p-value tells you nothing about the probability of a null hypothesis other than it is assumed true. Under a NHST p-value, $p (H_{0}) = 1.00$ .

Jacob Cohen outlines a nice example wherein he compares $p (D | H_{0})$ to the probability of obtaining a false positive on a test of schizophrenia. Given his hypothetical example, the prevalence of schizophrenia and the sensitivity and specificity of assessment tests for schizophrenia, an unexpected result (a positive test) is more likely to be a false positive than a true negative. You can read his paper here.

If you want $p (H_{0} | D)$ , you may need another route such as Bayesian Statistics.

6.1.3.2 2. Odds the alternative is true

In NHST, no likelihoods are attributed to hypotheses. Instead, all p-values are predicated on $p (H_{0}) = 1.00$ . It is assumed that the null is true. Thus, statements such as ‘ $1 - p$ indicates the probability $H_{A}$ is true’ is false.

6.1.3.3 3. Small p-values indicate large effects

This is not the case. p-values depend on other things, such as sample size, that can lead to statistical significance for minuscule effect sizes. For example, consider the results of the following two correlations:

Result from test 1:

r	p	Method
0.1	0.0015441	Pearson's product-moment correlation

Result from test 2:

r	p	Method
0.1	0.3222174	Pearson's product-moment correlation

In the above, the two tests have the exact same effect size and correlation statistics, $r = .1$ . However, the p-values vary substantially. Thus, effect size does not map directly onto p-value. One major other consideration is sample size. For extremely large sample sizes, a small effect size may have a small p-value (i.e., minor effect is statistically significant). For extremely small sample sizes, a large effect may have a large p-value (i.e., a major effect is not statistically significant).

As a result, it is important to not interpret p-values alone. Effect sizes and confidence intervals are much more informative.

6.2 Power

Whereas p-values rest on the assumption that the null hypothesis is true, the contrary assumption, that the null hypothesis is false (i.e., an effect exists), is important for determining statistical power. Statistical power is defined as the probability of correctly rejecting the null hypothesis given an true population effect size and sample size, or more formally:

Statistical power is the probability that a study will find p < $α$ IF an effect of a stated size exists. It’s the probability of rejecting $H_{0}$ when $H_{1}$ is true. (Cumming & Calin-Jageman, 2016)

See the following figure for a depiction, where alpha= $α$ and 1-beta = $1 - β$ = power:

This plot illustrates the concept of statistical power by comparing the null and alternative distributions. The red curve represents the null hypothesis ( $H_{0}$ ) distribution, which assumes no effect, while the blue curve represents the alternative hypothesis ( $H_{1}$ ) distribution, which assumes an effect with a mean shifted to 3. The light red shaded area under the null distribution beyond the critical value ( $\pm 1.96$ ) represents the Type I error rate ( $α$ ), or the probability of rejecting the null hypothesis when it is true.

In contrast, the dark blue shaded area under the alternative distribution to the left of the critical value represents the Type II error rate ( $β$ ), or the probability of failing to reject the null hypothesis when it is false. The light blue shaded region under the alternative distribution beyond the critical value reflects the statistical power ( $1 - β$ ), which is the probability of correctly rejecting the null hypothesis when it is false, thus detecting a true effect. Text annotations highlight key concepts: 1 - α represents the probability of correctly failing to reject the null hypothesis when it is true, 1 - β represents statistical power, α/2 marks the Type I error probability in each tail, and β indicates the probability of making a Type II error.

We can conclude from this definition that if your statistical power is low, you will not likely reject $H_{0}$ regardless of if there is a population-level effect (i.e., $H_{1} \neq 0$ ). As will be demonstrated, underpowered studies are doomed from the start. Conversely, if a study is overpowered (i.e., extremely large sample size), you can get a statistically significant result for what might be a infinitesimal or meaningless effect size.

Note

Before proceeding to the next example, please note that you will often see the symbol ‘rho’, which is represented by the Greek symbol $ρ$ (it’s a blend of r and o). This is the population parameter of a correlation. This is the not the same as a p-value, which is represented by the letter $p$ . It may get confusing it you mix up these symbols, so be sure you know the difference between the two.

Consider a researcher who is interested in the association substance use (SU) and suicidal behaviors (SB) in Canadian high school students. They design a study and use the NHST framework. Under this framework, they set the following hypotheses:

$H_{0} : ρ = 0$
$H_{1} : ρ \neq 0$

Let’s assume that the true correlation between SU and SB is $ρ = .3$ ; the researchers do not know that this is the true value. The population data might look like this:

Every faint gray dot represents a student. Their score on SU is on the y-axis, while their score on SB is on the x-axis. We can see a trend where students with higher SU also have higher, on average, SB. So, it appears that as substance use increases, so do suicidal behaviors. Although we aren’t so omniscient in the real world, the population correlation here is $ρ = .3$ .

However, before conducting the study, the researcher conducts a power analysis to determine an appropriate sample size required to adequately power their study. They want to have a good probability of rejecting the null, if it were false (here, we know this is the case). To calculate the appropriate sample size, they will require: 1) $α$ criterion level, 2) desired power ( $1 - β$ ), and 3) hypothesized effect size. The researcher uses the standard for $α$ criterion and power. Thus, they have: 1) $α = .05$ , 2) 1- $β$ = .8, and they estimate the true effect based on the literature to be 3) $ρ$ = .300. Although we know the population correlation and that the researcher has accurately estimated the population effect, researchers may not accurately estimate the population effect size. In real-world research we would need to find a good estimate of the effect size, which is typically through reading the literature for effect sizes in similar populations. Power can be calculated using R or GPower. Using R, the researcher uses the pwr package to conduct their power analysis. This package is very useful; you can insert any three of the required four pieces of information (alpha, power, estimated sample size, and sample size) to calculate the missing piece. More details on using pwr are below. For our analysis, we get:


     approximate correlation power calculation (arctangh transformation) 

              n = 84.07364
              r = 0.3
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

The results of this suggest that we need a sample of about 85 people (rounding up from $n = 84.07$ ) to achieve our desired power ( $1 - β = 0.8$ ), using our known population correlation ( $ρ = .3$ ) and $α = .05$ .

What does this mean? It means that if the true population correlation was $ρ = .3$ , then about 80% of all hypothetical studies using a sample size of $n = 85$ drawn from this population will yield $p < α$ .

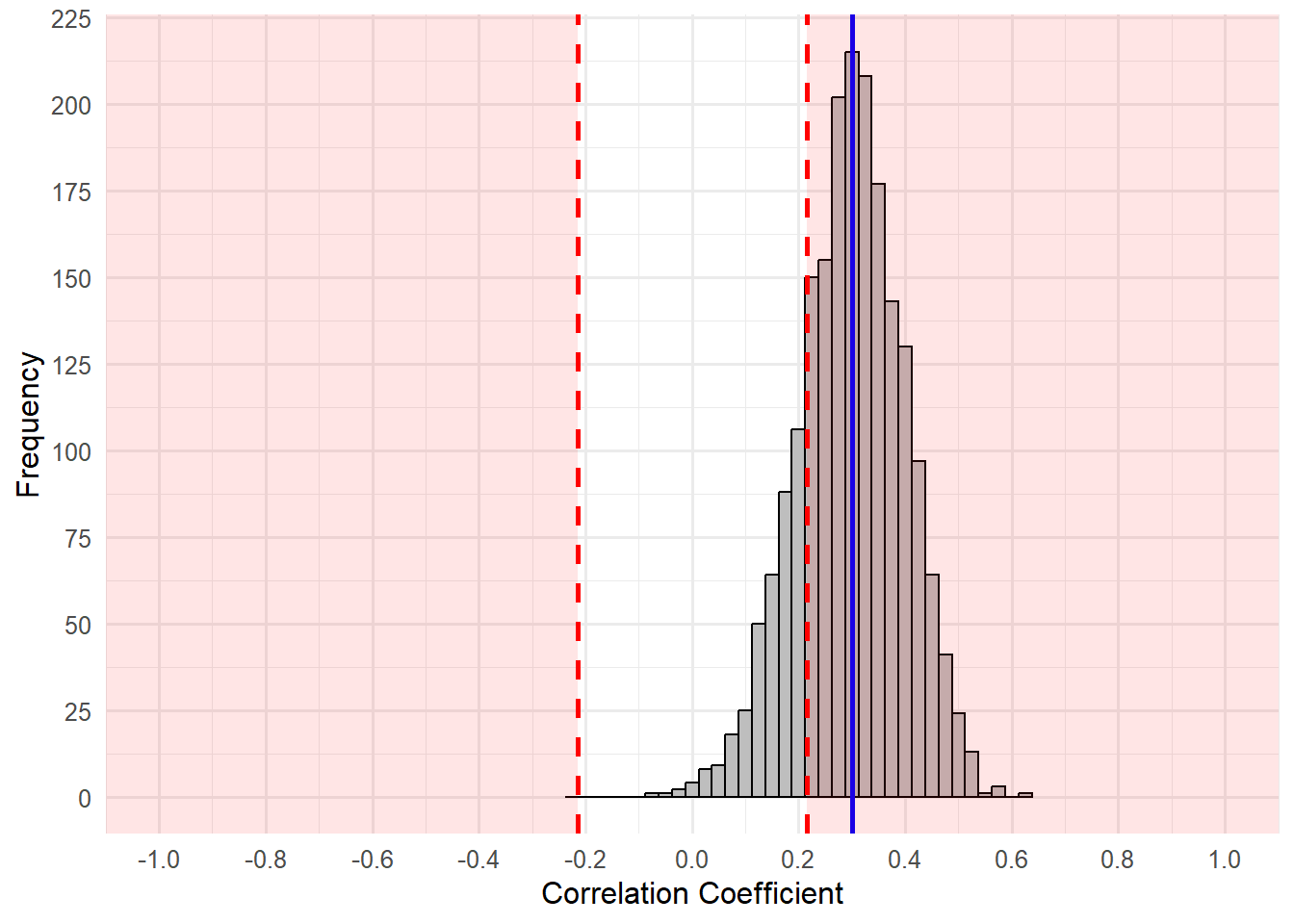
We can create a histogram that plots the results of many random studies ( $n = 85$ ) drawn from our population to determine which meet $p < α$ :

This graph represents the distribution of correlation coefficients for each of our random samples, which were drawn from our population. Notice how they form a seemingly normal distribution around our true population correlation coefficient, $ρ = .300$ . Although it may seem normal, it is actually skewed because of the bounds of the correlation (i.e., -1 to 1).

The red lines and shaded regions represent correlation coefficients that are beyond the $r = .215$ cut-off, which represent the extreme 5% (2.5% per tail) of sample under a true null and, thus, would result in $p < .05$ . The blue line represents the true population correlation coefficient ( $ρ = .300$ ). Just how many samples scored at or beyond the critical correlation value of $r = .215$ ? Think about it before proceeding.

The results of our correlations suggest that 1609 correlation coefficients were at or beyond the critical value. Do you have any guess what proportion of the total samples that was? Recall that power is the probability that any study will have $p < α$ . Approximately eighty percent (80.45%) of these studies met that criteria: this was our power! Why is it 80.45 and not 80% exactly? Remember, power refers to a hypothetically infinite number of samples drawn from the population, for any given sample size, effect size, and $α$ . Had we drawn $\infty$ samples, we would have 80% having $p < α$ . Also, recall that we rounded up to 85 people per sample, not 84. Having more people will result in higher power, holding all other things constant. Rounding down would have lower power below $1 - β = .8$ and a sample size of $n = 84.07$ is impossible. Thus, rounding up is the best course of action.

6.2.1 What if we couldn’t recruit 85 participants?

Perhaps we sampled from one high school in a small Canadian city and could only recruit 32 participants. How do you think this would affect our power? First, smaller sample sizes give less precise estimations of population parameters under the alternative distribution (i.e., the histogram above of distribution of sample statistics may be more spread out).

Second, this also influences our critical region for the correlation coefficient, so the red regions shift outward. That is, a lower sample size also increase variability in the distribution of sample statistics for the null distribution, as well. This means that the extreme 5% will be further out. Overall, both of these reduce power.

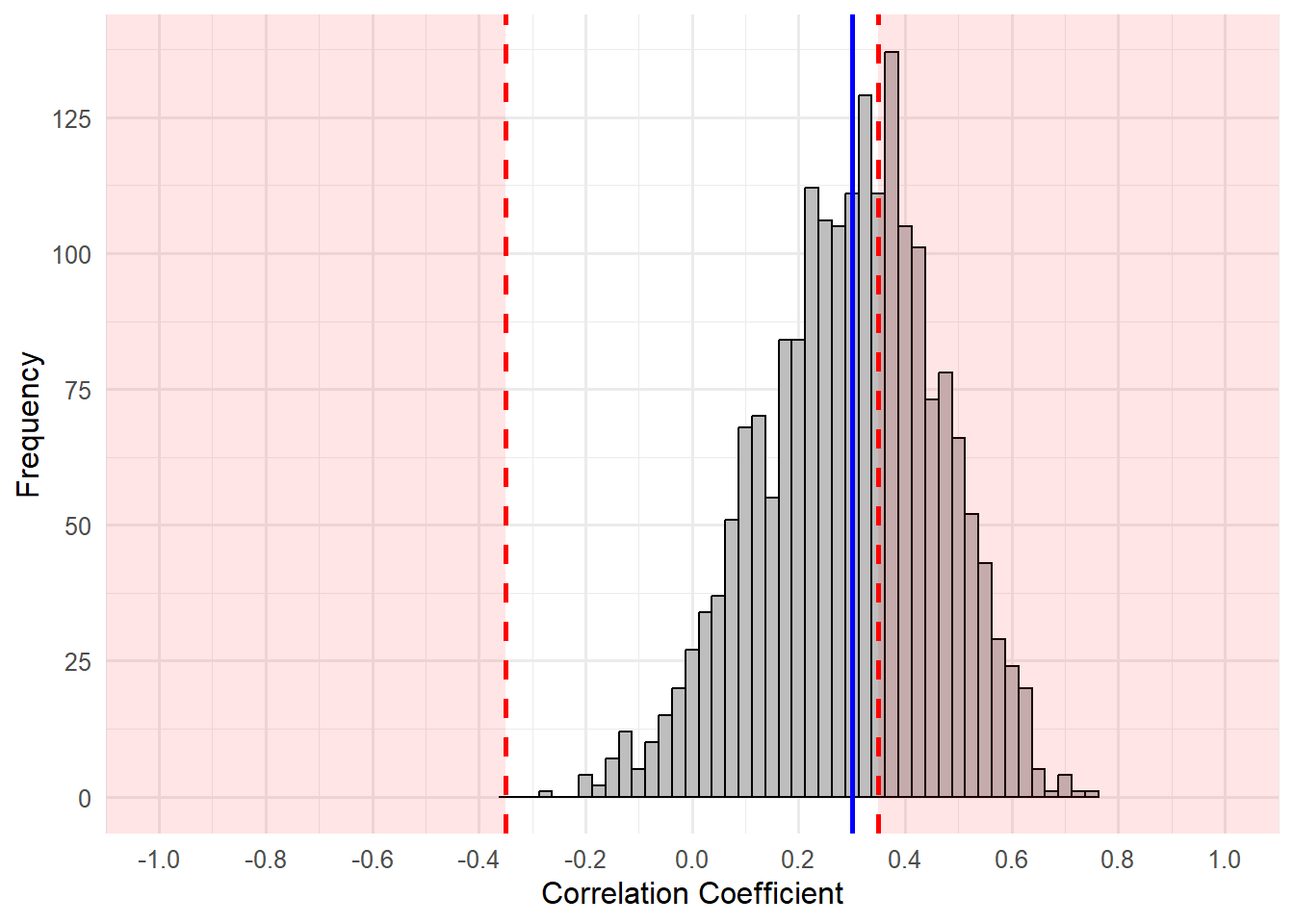
Let’s rerun our simulation with 2,000 random samples of $n = 32$ to see how it affects out power. Remember, the true population effect is $ρ = .3$ . We can plot the resultant correlation coefficients. Note that the critical correlation coefficient value for $n = 32$ is more narrow for $n = 85$ compared to $n = 32$ . The new critical value is $r = 349$ (compared to $r = 215$ ). The following figure represents the 2,000 samples:

Hopefully, you can see that despite the distribution still centering around the population correlation of $ρ = .3$ , it has spread out more. We are less precise in our estimate. Furthermore, the red region (critical r region) is shifted outward due to a smaller $n$ . This would mean that fewer of the samples result in correlation coefficients that fall in the red regions and be statistically significant (i.e., power is lower). Would a formal power calculation agree? First, let’s find out how many studies resulted in $p < α = .05$ and then do a formal power analysis to determine if they are equal.

Our results suggest that of the 2000 simulated studies, 792 studies yielded statistically significant results ( $792 / 2000 = 39.6 %$ ). Would our power align?

Formal Power Analysis


     approximate correlation power calculation (arctangh transformation) 

              n = 32
              r = 0.3
      sig.level = 0.05
          power = 0.3932315
    alternative = two.sided

Whoa! Power was $1 - β = .3932$ (i.e., 39.32% of samples). Close enough!

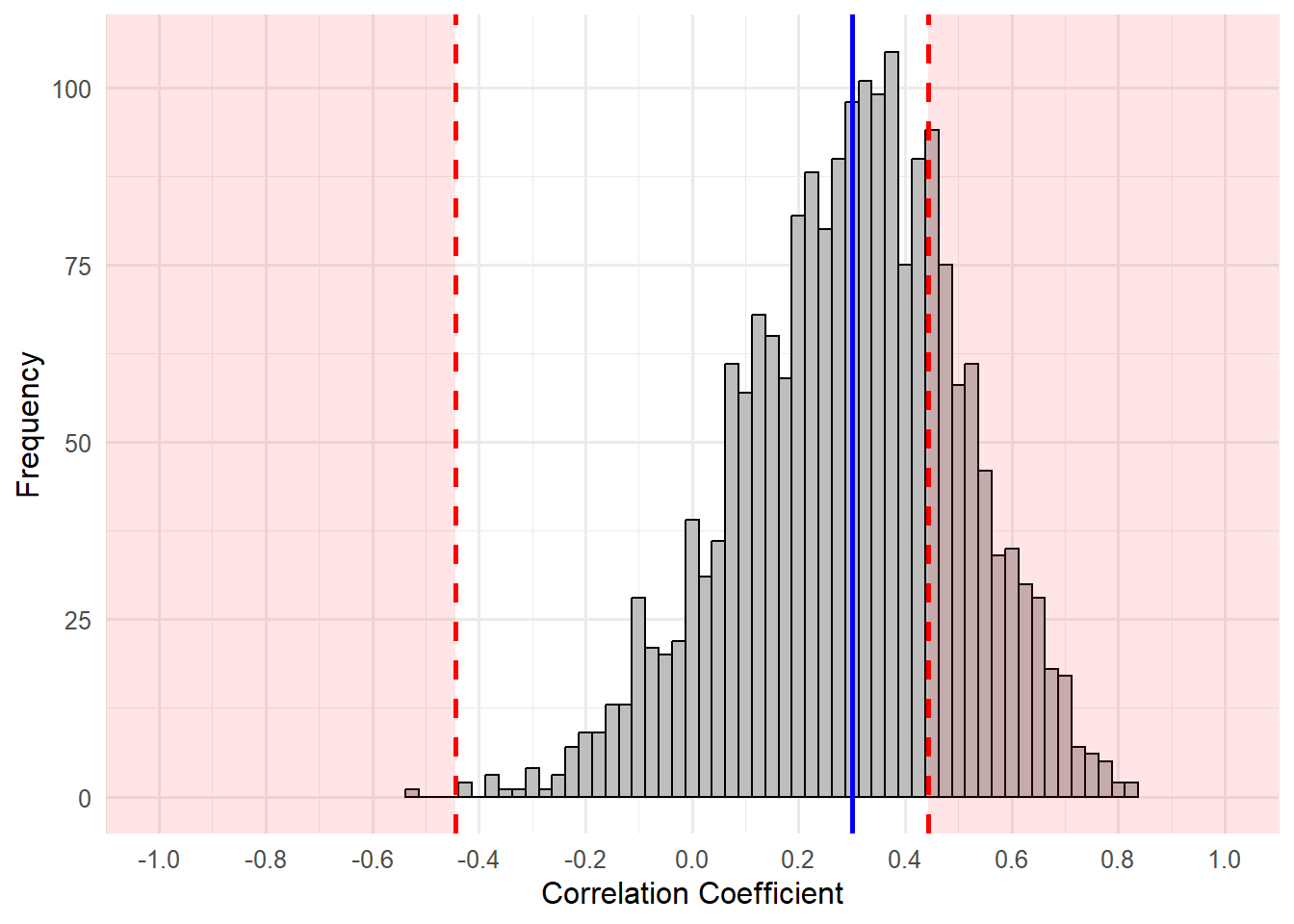
Let’s take it one step further and assume we could only get 20 participants. This is the plot of the resultant correlation coefficients. Note that the critical correlation coefficient value for $n = 20$ is larger than for $n = 32$ (remember that the null distribution or samples would be spread out more for smaller sample sizes). The new critical value is $r = 444$ . The following is adjusted for 20 participants:

Hopefully, you can see that despite the distribution still centering around our population correlation of .3, the red regions are further outward than the previous two examples. Again, let’s see how many studies resulted in $p < α = .05$ and then do a formal power analysis to determine if they are equal.

A total of 496 studies yielded statistically significant results ( $510 / 2000 = 25.5 %$ ). More, you may even notice that in the previous figure, a statistically significant result occurred in the opposite direction (look in the left red region). That is, some results would suggest a negative correlation despite the true parameter being positive. Would a formal power analysis align?


     approximate correlation power calculation (arctangh transformation) 

              n = 20
              r = 0.3
      sig.level = 0.05
          power = 0.2559237
    alternative = two.sided

So, out of 2000 random samples from our population, 25.5% had $p < α = .05$ and our power analysis suggests that 25.6% would. Again, given infinite samples, there would be 25.59237…% with $p < α = .05$ .

In sum, as sample size decreases and all other things are held constant, our power decreases. If your sample is too small, you will be unlikely to reject $H_{o}$ even if a true effect exists. Thus, it is important to ensure you have an adequately powered study. Plan ahead. Otherwise, even if a population effect exists, you may not conclude that through NHST’. Or, maybe a non-NHST approach is best.

6.3 Increasing Power

Power is the function of three components: sample size, hypothesized effect, $a l p h a$ . Thus, power increases:

When the hypothesized effect is larger;
When you can collect more data (increase $n$ );
or by increasing your alpha level (i.e., making it less strict).

This relationship can be seen in the following graphs:

$α = .05$

$α = .01$

$α = .001$

Check the Graphs

Compare the various rhos within a graph.

Also compare the rhos betwen a graph.

6.3.1 Effect Size

As the true population effect reduces in magnitude, your power is also reduced, given constant $n$ and $α$ . So, if the population correlation between substance abuse and suicidal behaviors was $ρ = .1$ , we would require approximately $n = 782$ to achieve power of $1 - β = .8$ . In other words, 80% of hypothetically infinite number of samples of $n = 782$ would give statistically significant results, $p < α$ , when $ρ = .1$ .

If the population correlation was $ρ = .05$ , we would require approximately $n = 3136$ to achieve the same power. This is the basis of the argument that large enough sample sizes result in statistically significant results, $p < α$ , that are meaningless (from a practical/clinical/real world perspective). If $ρ = .05$ , which is a very small and potentially meaningless effect, large samples will likely detect this effect and result in statistical significance. Hypothetically, 80% of the random samples of $n = 3136$ will result in $p < α = .05$ for a population correlation of $ρ = .05$ . Despite the statistical significance, there isn’t much practical or clinical significance. Statistical significance $\neq$ practical significance.

6.3.1.1 Ways to Estimate Population Effect Size

There are many ways to estimate the population effect size. Here are some common examples, ordered by recommendation:

Existing Meta-Analysis Results
Meta-analyses compile and combine results from multiple studies to give a more accurate estimate of the population effect size. By aggregating data across various studies, meta-analyses reduce bias and provide a more stable estimate.
- Recommendation: Use the lower-bound estimate of the confidence interval (CI) from the meta-analysis. This is a more conservative approach that accounts for uncertainty and publication bias, which helps avoid overestimating the true effect size.
- Why it’s recommended: Meta-analyses offer a robust estimate by synthesizing evidence from multiple studies. Using the lower bound ensures a conservative sample size calculation, reducing the risk of underpowering your study.
Existing Studies with Parameter Estimates
When no meta-analysis is available, individual studies reporting effect size estimates can be used. These should come from studies with similar designs, populations, or theories.
- Recommendation: Use the lower-bound estimate of the confidence interval presented in the study or halve the reported effect size from a single study to ensure a more conservative estimate.
- Why it’s recommended: Single studies are more prone to sampling variability and biases like publication bias. By halving the effect size or using the lower bound, you reduce the risk of overestimating the true population effect size.
Smallest Meaningful Effect Size Based on Theory
Theoretical frameworks can suggest the smallest effect size that would be considered meaningful or practically important in your study. This might come from expert consensus or previous theoretical work that identifies thresholds for meaningful differences.
- Recommendation: Choose the smallest effect size that is theoretically or practically significant. This ensures your study has enough power to detect meaningful effects, even if they are small.
- Why it’s recommended: Aligning effect size with theoretical relevance ensures your study detects effects that are practically or theoretically important rather than insignificant.
General Effect Size Determinations (Small, Medium, Large)
If no specific guidance is available, general benchmarks for effect sizes can be used:
- Small: Cohen’s d = 0.2, Pearson’s r = 0.1
- Medium: Cohen’s d = 0.5, Pearson’s r = 0.3
- Large: Cohen’s d = 0.8, Pearson’s r = 0.5
- Recommendation: Choose the general effect size that aligns best with your theory. If a strong relationship is expected, use a larger effect size; if subtle, use a smaller one.
- Why it’s recommended: These general benchmarks provide a starting point when no other data is available. They help design studies with realistic expectations for effect sizes, even without prior research.

6.3.2 $α$ level

Recall that the alpha level (commonly set at 0.05) represents the threshold we choose to determine statistical significance. Specifically, it is the probability of committing a Type I error — rejecting the null hypothesis when it is actually true. In other words, it defines the “extreme” region of our null distribution, where we would reject the null hypothesis in favor of the alternative hypothesis.

6.3.2.1 Reducing Alpha and Its Consequences

When we reduce our alpha level, we are essentially making our criterion for rejecting the null hypothesis more strict. This means that fewer observed outcomes will fall into the “extreme” region, which is now smaller. Visually, this reduction in alpha shrinks the size of the red areas in a power curve (those areas representing where we reject the null hypothesis under the alternative distribution). These areas are associated with detecting true effects, so shrinking them decreases the likelihood of finding a significant result when an effect is present.

Increased Threshold for “Extreme” Results: Lowering alpha increases the critical value (e.g., a larger correlation coefficient or test statistic would be needed to reject the null hypothesis). In the case of correlation tests, this results in a larger correlation coefficient threshold that we consider “extreme” enough to indicate significance. Essentially, we are raising the bar for what qualifies as a significant result.
Decreased Statistical Power: Holding all other factors constant, reducing the alpha level will decrease the power of the test. Power refers to the probability of correctly rejecting the null hypothesis when it is false (i.e., detecting a true effect). As the threshold for significance becomes stricter, it becomes harder to detect effects because the criterion for rejection is less lenient. Consequently, more true effects may go undetected, increasing the risk of committing a Type II error (failing to reject a false null hypothesis).

6.3.2.2 Trade-offs in Reducing Alpha

Reducing alpha is often done to minimize the risk of a Type I error, but this comes with trade-offs. While a stricter alpha reduces the probability of falsely rejecting the null hypothesis, it also reduces the power of your test, making it harder to detect true effects. Therefore, when designing a study, it’s important to carefully balance the chosen alpha level with the desired power, especially when small effects are being studied.

For instance: - If alpha is set too low (e.g., .01 instead of the conventional .05), the critical value becomes much larger, and your study may require a larger sample size to maintain sufficient power. - If alpha is too lenient (e.g., .10), the power may increase, but this comes at the expense of a higher likelihood of committing a Type I error, which could undermine the validity of your findings.

Thus, reducing alpha lowers the probability of Type I errors but also decreases the test’s power, making it more difficult to detect real effects. This trade-off must be carefully considered during the study design phase, particularly in studies where detecting small but meaningful effects is crucial.

6.4 Afterward

This section will focus on conducting power analysis across various statistical platforms.

6.4.1 Power in R

We will focus on two packages for conducting power analysis: pwr and pwr2.

6.4.1.1 Correlation

Correlation power analysis has four pieces of information. You need any three to calculate the other:

n is the sample size
r is the population effect, $ρ$
sig.level is you alpha level
power is power

So, if we wanted to know the required sample size to achieve a power of .8, with a alpha of .05 and hypothesized population correlation of .25:


     approximate correlation power calculation (arctangh transformation) 

              n = 122.4466
              r = 0.25
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

6.4.1.2 t-test

With same sized groups we use pwr.t.test. We now need to specify the type as one of ‘two.sample’, ‘one.sample’, or ‘paired’ (repeated measures). You can also specify the alternative hypothesis as ‘two.sided’, ‘less’, or ‘greater’. The function defaults to a two sampled t-test with a two-sided alternative hypothesis. It uses Cohen’s d population effect size estimate (in the following example I estimate population effect to be $d = .3$ :


     Two-sample t test power calculation 

              n = 175.3847
              d = 0.3
      sig.level = 0.05
          power = 0.8
    alternative = two.sided

NOTE: n is number in *each* group

6.4.1.3 One way ANOVA

One way requires Cohen’s F effect size, which is kind of like the average Cohen’s d across all conditions. Because it is more common for researchers to use $η_{2}$ , you may have to convert something reported fro another study. You can convert $η_{2}$ to $F$ with the following formula:

Cohen’s F $= \sqrt{\frac{η^{2}}{1 - η^{2}}}$

pwr.anova.test() requires the following:

k = number of groups
f = Cohen’s F
sig.level is alpha, defaults to .05
power is your desired power


     Balanced one-way analysis of variance power calculation 

              k = 3
              n = 21.10364
              f = 0.4
      sig.level = 0.05
          power = 0.8

NOTE: n is number in each group

6.4.2 Alternatives for Power Calculation

6.4.2.1 G*Power

You can download here.

6.4.2.2 Simulations

Simulations can be run for typical designs, which you have seen above through our own simulations to demonstrate the general idea of power. For example, we can repeatedly run a t-test on two groups with a specific effect size at the population level. Knowing that Cohen’s d is:

$d = \frac{{\overset{―}{x}}_{1} - {\overset{―}{x}}_{2}}{s_{p o o l e d}}$

We can use rnorm() to specify two groups where the difference in means is equal to Cohen’s d and when we keep the SD of both groups to 1.


    Two Sample t-test

data:  rnorm(sample_size) and rnorm(sample_size, mean = cohens_d)
t = 0.039978, df = 38, p-value = 0.9683
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.6019724  0.6262270
sample estimates:
mean of x mean of y 
0.2923802 0.2802529

We can use various R capabilities to simulate 10,000 simulations and determine the proportion of studies that conclude that $p < α$ .

This returned a data.frame will 10,000 pvalues from simulations. The results suggest that 2360 samples were statistically significant, indicating 23.6% were statistically significant.

You may be thinking, why do this when I have pwr.t.test? Well, the rationale for more complex designs is the same. For more complicated designs, it can be difficult to determine the best power calculation to use (e.g., imagine a 4x4x4x3 ANOVA or a SEM). Sometimes it makes sense to run a simulation.

Simulation of SEM in R, which can help with power analysis.

Companion shiny app regarding statistical power can be found here.

6.5 Recommended Readings:

Cohen, J. (1994). The Earth is round (p < .05).American Psychologist, 49, 997-1003.
Nickerson, R. S. (2000). Null hypothesis significance testing: A review of an old and continuing controversy. Psychological Methods, 5(2), 241–301. https://doi.org/10.1037/1082-989x.5.2.241
Pritchard, T. R. (2021). Visualizing Power.

6.1 p-values

6.1.1 If the null hypothesis is true, why would our data be extreme?

6.1.2 Why is α=.05

6.1.3 Misconceptions

6.1.3.1 1. Odds against chance fallacy

6.1.3.2 2. Odds the alternative is true

6.1.3.3 3. Small p-values indicate large effects

6.2 Power

6.2.1 What if we couldn’t recruit 85 participants?

6.3 Increasing Power

6.3.1 Effect Size

6.3.1.1 Ways to Estimate Population Effect Size

6.3.2 α level

6.3.2.1 Reducing Alpha and Its Consequences

6.3.2.2 Trade-offs in Reducing Alpha

6.4 Afterward

6.4.1 Power in R

6.4.1.1 Correlation

6.4.1.2 t-test

6.4.1.3 One way ANOVA

6.4.2 Alternatives for Power Calculation

6.4.2.1 G*Power

6.4.2.2 Simulations

6.5 Recommended Readings:

6.1.2 Why is $α = .05$

6.3.2 $α$ level