12  Repeated Measures ANOVA

This chapter will cover the repeated measures ANOVA, a statistical method used to determine if there is a significant difference among the means of three or more related groups. Unlike a one-way ANOVA, which involves independent groups, a repeated measures ANOVA is used when the same participants are measured under different conditions or at different time points. The repeated measures design accounts for the correlation between the measurements from the same participants. For example, if we compare the heights of various children over time, we would assume that children who are tall will grow into adults who are tall, and children who are short will grow into adults who are short. Or, as another example, imagine we test the impact of various sports drink on speed. If we gave the same participant three different sports drinks and tested their running speed after each, that person’s scores would be dependent or correlated. Fast people will typically be fast and slower people will typically be slow, regardless of the drink given. This dependence or correlation of observations is why the working with repeated measures data requires specific assumptions and analysis.

12.1 Some Additional Details

The repeated measures ANOVA is appropriate when there is one independent variable (IV) with three or more levels (e.g., conditions or time points) and one continuous dependent variable (DV). For example, researchers might use a repeated measures ANOVA to compare test scores (DV) across three different time points (IV with three levels) or to assess the effects of a three different treatments (IV with three levels) on pain (DV). Importantly, the same participants are measured at each level of the IV.

Note

Sometimes a repeated measures design can be used on different people, but when they are matched on various important characteristics. In this chapter and course we will assume the same people measured across conditions or time.

The null hypothesis for the repeated measures ANOVA posits that all group means are equal across different conditions or time points:

\[ H_0: \mu_1 = \mu_2 = \mu_3 = \ldots = \mu_k \]

where \(k\) represents the number of conditions or time points. The alternative hypothesis states that at least one group mean is different:

\[ H_1: \text{At least one } \mu_i \text{ differs from another} \]

By rejecting the null hypothesis, researchers conclude that significant differences exist among the conditions or time points–at least one differs from the others. Similar to a one-way ANOVA, post hoc tests are often required to identify where these differences occur.

12.1.1 Key Assumptions

A repeated measures ANOVA can be conducted under certain assumptions. These include:

12.1.1.1 1. The data are continuous

The dependent variable should be at the interval or ratio level.

12.1.1.2 2. Sphericity

Sphericity is a key assumption in repeated measures ANOVA. It refers to the equality of variances of the differences between all possible pairs of conditions or time points. For example, consider the following scores representing five people who were all given three different interventions for depressive symptoms.

ID Treatment.1 Treatment.2 Treatment.3
1 6 10 11
2 8 11 17
3 7 14 15
4 10 16 23
5 13 15 21

We can calculate the differences (one subtracted another) of each pair of scores per person. For example, consider treatment 1 and 2:

ID Treatment.1 Treatment.2 Difference_1_2
1 6 10 -4
2 8 11 -3
3 7 14 -7
4 10 16 -6
5 13 15 -2

We can calculate a variance of these difference scores, which would be 4.3. Well, the test of sphericity tests if the variance between ALL possible difference scores (here, 1 - 2, 2 - 3, and 1 - 3) is similar. The repeated measures ANOVA requires these variances be similar, and Mauchley’s test of sphericity is the formal test for this. For example, the variances of the differences are:

  1. Treatment 1 - Treatment 2 = 4.3
  2. Treatment 2 - Treatment 3 = 8.7
  3. Treatment 1 - Treatment 3 = 8.3

So, while the variances quite obviously are not equally, the sphericity test is a formal test to ensure we meet or do not meet this assumption.

In simpler terms, sphericity assumes that the relationship (or correlation) between scores in different conditions is consistent. This assumption is unique to repeated measures designs because the same participants contribute data across multiple conditions, introducing dependencies in the data.

If the assumption of sphericity is violated, the repeated measures ANOVA can lead to inflated Type I error rates, meaning there’s a higher chance of incorrectly rejecting the null hypothesis.

12.1.1.2.1 Testing for Sphericity

Sphericity can be tested using Mauchly’s test of sphericity. This test evaluates whether the variance of the differences between groups is equal. This test has the following hypotheses:

  • Null hypothesis (\(H_0\)): The variances of the differences between all pairs of conditions are equal (sphericity holds).
  • Alternative hypothesis (\(H_1\)): The variances of the differences are not equal (sphericity is violated).

If Mauchly’s test is significant (\(p < .05\)), sphericity is violated. When this happens, adjustments to the degrees of freedom (df) are required to make the test more robust. Specifically, when sphericity is violated, the F-statistic becomes unreliable. To address this, two common corrections can be applied:

  1. Greenhouse-Geisser Correction:
    • This is a conservative adjustment.
    • It reduces the degrees of freedom based on an estimated epsilon (\(\epsilon\)) value, which quantifies the degree of violation.
    • Lower values of \(\epsilon\) indicate greater violations of sphericity (with \(\epsilon = 1\) indicating perfect sphericity).
  2. Huynh-Feldt Correction:
    • This is a less conservative adjustment compared to Greenhouse-Geisser.
    • It adjusts the degrees of freedom based on a different estimation of \(\epsilon\), which can be slightly larger.

When reporting results of the repeated measures ANOVA, it’s standard to use corrected degrees of freedom and note which correction was applied. ANOVA results will typically inform you which degrees of freedom go with which correction. Sometimes the degrees of freedom may not be whole numbers.

12.1.1.3 3. Homogeneity of variances

The variance within each group should be approximately equal. This assumption is less of a concern than in a one-way ANOVA, but it’s still important to check. As with one-way ANOVA, Levene’s test can be used to assess this.

12.1.1.4 4. Normality of residuals

As with one-way ANOVA, it’s the residuals (the differences between the observed and predicted values) that should be normally distributed. This can be assessed visually using a Q-Q plot or by conducting a Shapiro-Wilks test on the residuals.

We will now go through a comprehensive example of a research project that requires the use of a repeated measures ANOVA.

12.2 Remember Me?

You are hired by the Reach Out Center for Kids (ROCK) as a developmental researcher as part of their cognitive development team. You are tasked with conducting research investigating the changes in memory processes across early childhood. Specifically, you believe that the amount of ‘chunks’ of memory a child can retain increases as children grow. You decide to develop a memory test to assess any changes over time. After reading the literature, you and your team believe that memory will improve as children develop. Importantly, you believe that notable changes will be evident between children when they are 4, 6, and 8-years old.

12.3 Step 1. Generate Hypotheses

The main null and alternative hypotheses for this repeated measures ANOVA can be converted into a statistical hypothesis stated as (for the null):

\[ H_0: \mu_{4yo} = \mu_{6yo} = \mu_{8yo} \]

And (for the alternative):

\[ H_1: \text{At least one } \mu_i \text{ differs from the others.} \]

12.4 Step 2. Designing the Study

You and your team plan out a research study. The method follows:

Participants: Participants were recruited from local schools near ROCK. Posters were created in collaboration with the school board, ensuring all parties agreed on recruitment materials. Eligible participants were children who were typically developing and had no reported neurological or developmental disorders. Children were tested when they are aged 4, 6, and 8 years old.

A power analysis was conducted using your literature review and indicated that a total of 12 children will be needed to achieve a power of \(1-\beta=.8\).

Materials: Tyler’s Memory Test (TMT; Pritchard, 2024) was used to assess memory. The TMT is a child-friendly memory that measures children’s total overall memory. The tasks involved recalling: items from a story presented with accompanying pictures, series of digits, and abstract shapes through drawing. The test is standardized and compared children’s scores to same-aged peers. Memory performance was scored out of 10. The TMT has shown suitable reliability and validity (Pritchard, 2024).

Procedure: Posters advertisements were shared on ROCK’s website, in addition to the researchers’ social media pages. The poster focused on caregivers of 4-year olds and indicated they could participate in a study on memory. Interested caregivers were provided an informed consent form and, once consenting, completed a brief screener to ensure children did not meet criteria for neurological or other psychological disorder. The resulting participants completed three memoery sessions (at age 4, 6, and 8 years old) at ROCK’s testing center. All testing was completed by PhD-level psychologists. Parents provided debriefed after each testing session.

The ethics review board at Grenfell Campus reviewed the project and ethics submission and approved the study.

12.5 Step 3. Conducting the Study

The study was completed as described; a final sample size of 8 was used. The following data were obtained:

Memory Scores Over Time
ID Age 4 Age 6 Age 8
1 3 5 7
2 4 3 8
3 3 5 5
4 3 3 8
5 4 4 7
6 4 4 9
7 1 4 7
8 2 3 8

12.6 Our Model

In previous examples of ANOVA, we have had different individuals for each level or condition. Recall that in the one way ANOVA example, each individual received one type of therapy. However, sometimes it makes sense to put the same individuals in each condition to assess change or differences within the individuals. Repeated measures do just that.

As such, our model will look similar:

\(memory = age + error\)

and for each individual:

\(y_i=age_i+e_i\)

12.7 Assumptions

Importantly, one of the major assumptions of the ANOVA is that the observations or independent. This is automatically violated in repeated measures. Despite repeated measures being a strength because it helps us attribute changes to experimental conditions, it is a violation of the assumptions under which our F test was based.

12.7.1 Sphericity

To allows us to continue with F-tests, we must introduce an additional assumption: sphericity and compound symmetry. In short, this assumption purports that the variance of the differences between all conditions is the same and covariances between individuals between conditions is also similar.

An easy way to visualize this is by plotting difference scores. In our example, we will have three difference scores (i.e., age 4 - age 6; age 6 - age 8; age 4 - age 8).

Memory Scores Over Time
ID Age 4 Age 6 Age 8 4 - 6 6 - 8 4 - 8
1 3 5 7 -2 -2 -4
2 4 3 8 1 -5 -4
3 3 5 5 -2 0 -2
4 3 3 8 0 -5 -5
5 4 4 7 0 -3 -3
6 4 4 9 0 -5 -5
7 1 4 7 -3 -3 -6
8 2 3 8 -1 -5 -6

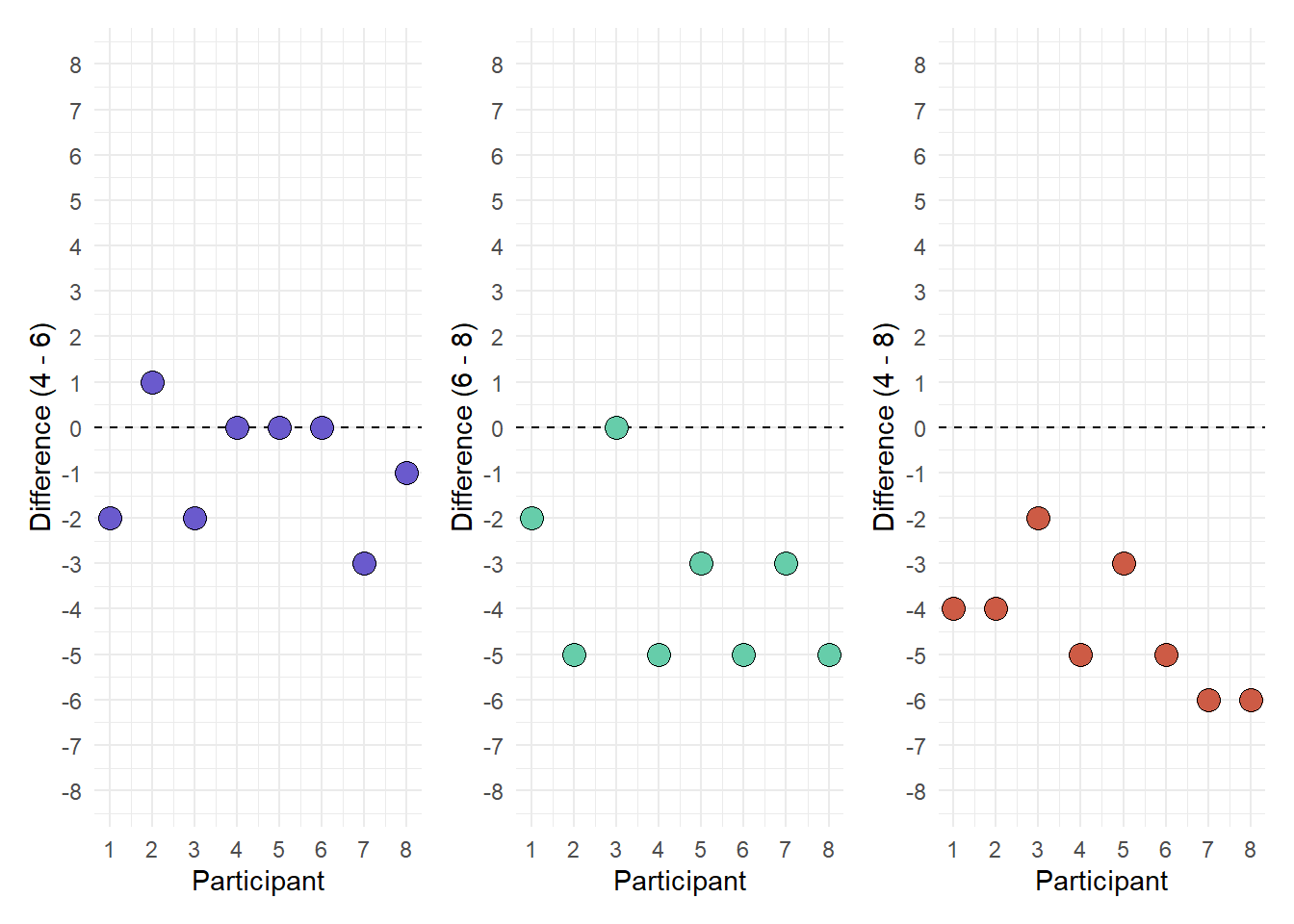
In the visualization we want to look at the dispersion along the y-axis. It should appear similar across the group differences. The variance of each of the differences is:

  • Four - Six: 1.839
  • Six - Eight: 3.429
  • Four - Eight: 1.982

We can test the assumption using Mauchly’s test of Sphericity, which hypothesizes (for a three condition repeated measures deign):

\(H0: \sigma^2_{A-B}=\sigma^2_{A-C}=\sigma^2_{B-C}\)

\(H1:\) var not all equal.

We will not be concerned with the formal calculations of Mauchly’s test; rather, our statistical software can conduct it for us.

For our data:

  Effect         W         p p<.05
2    Age 0.8235094 0.5584776

Recall that the null hypothesis is that the variances are equal; thus, we want p>.05 for Mauchly’s test, although it’s not a complete deal-breaker if we violate this assumptions.

Regardless, our results indicate that we have not violated this assumption and can proceed as intended.

Our data:

We used Mauchly’s test to check the assumption of sphericity and the results indicate that the assumption is not violated, \(p = .558\).

You can apply two corrections to the data that account for violations of sphericity. These are the Greenhouse-Geisser or Huynh-Feldt corrections.

12.8 Our Analysis

As we have done in the last two chapters, we will partition the various into various subcomponents to determine the appropriate F statistic. The following holds:

You may recall that for independent ANOVAs the individuals in each condition were different. For repeated measures, the individuals will cut across all conditions. So why would they score differently on the same dependent variable? From the figure above, some of the differences may be due to the experiment, while others are just error. It may be helpful to re-conceptualize how we consider variance as the variance between and the variance within an individual. Because all people are in all conditions, changes within an individual can be attributed to the experimental condition and some error.

Let’s calculate some of these and it may help them make sense.

12.8.1 SST

Our total sum of squares is no different than a one way ANOVA.

\(SST=\sum_{i=1}^n(x_i-\overline{x}_{grand})^2\) with \(N-1\) degrees of freedom.

Also, if you know the variance, it can be calculated as:

\(SST=s_{overall}^2(N-1)\)

Our variance in all scores is 4.717 with \(n=24\). Thus:

\(SST=4.717(24-1)=108.49\)

12.8.2 SSW

Here we will depart from our independent ANOVA method. We will calculate the SSW by looking at the deviations within individuals (rather than within groups, which was error in the independent ANOVAs). Recall our data:

Memory Scores Over Time
ID Age 4 Age 6 Age 8
1 3 5 7
2 4 3 8
3 3 5 5
4 3 3 8
5 4 4 7
6 4 4 9
7 1 4 7
8 2 3 8

So, let’s consider individual \(1\). Their mean score is \(\frac{3+5+7}{3}=5\). And their deviations are:

\(SS_{x_{i=1}}=(3-5)^2+(5-5)^2+(7-5)^2=8\)

We do this across all individuals! The resulting formula is expressed as:

\(SSW=\sum_{i=1,t=1}^n(x_{it}-\overline{x}_{i})^2\)

where \(x_{it}\) is the score for individual \(i\) at time \(t\) and \(\overline{x}_{i}\) is the mean for individual \(i\) across all conditions. If you can quickly get the variances, you could also use the formula:

\(SSW=\sum_{i=1}^ns_{i}^2({n_{t}-1)}\)

For us, we have:

ID Variance
1 4.000000
2 7.000000
3 1.333333
4 8.333333
5 3.000000
6 8.333333
7 9.000000
8 10.333333

and thus, because each individual has three time points:

\(SSW=4(2)+7(2)+1.33(2)+8.33(2)+3(2)+8.33(2)+9(2)+10.33(2)=102.64\)

12.8.3 SSM

The variance of the model, SSM, which is between groups (i.e., experimental conditions) is calculated the same way as before).

\(SSM = \sum_{j=1}^{n_j}{n_j}(\overline{x}_j-\overline{x}_{overall})^2\)

For us, the means are:

Age Mean n
Mem_4 3.000 8
Mem_6 3.875 8
Mem_8 7.375 8

Therefore, because we know our grand mean is 4.75:

\(SSM=8(3.00-4.74)^2+8(3.875-4.74)^2+8(7.375-4.74)^2=85.74\)

12.8.4 SSE

Our error is calculated by removing the SS from the model from within individuals. Remember, individual scores vary because of the experimental conditions (i.e., SSM) and due to error (i.e., random individual fluctuations). Thus, the error can be calculated by subtracting SSM from SSW.

\(SSE=SSW-SSB\)

\(SSE=102.64-85.74=16.90\)

Perhaps now you see an added benefit to repeated measures designs. We have effectively reduced our error term.

12.8.5 Mean Squares

Our mean squares are calculated the same as before. However, our \(df_{e}\) is calculated by \(df_{e}=df_{w}-df_{b}\), where \(df_{w}=n_i(df_{b})\). We have eight individuals with \(df_b=2\), therefore \(df_w=8(2)=16\) and \(df_e=16-2=14\)

\(MSB = \frac{SSB}{df_b}\)

\(MSB = \frac{85.74}{2}=42.87\)

and

\(MSE = \frac{SSE}{df_e}\)

\(MSE = \frac{16.90}{14}=1.207\)

12.8.6 F Statistic

Our F statistic is calculated the same way as before, a ratio of MSB and MSE.

\(F=\frac{MSB}{MSE}=\frac{42.87}{1.207}=35.52\)

We can use an F-distribution table to find out our approximate \(p\)-value. We determine that \(F_{crit}(2, 14)=3.7389\).

However, remember, an ombinus ANOVA does not tell us where the differences are. We have three groups, so we must conduct post-hoc analysis. We looked at this in the one way and factorial ANOVA, so please refer there.

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = Memory ~ Age, data = dat_child_long)

$Age
             diff        lwr      upr     p adj
Mem_6-Mem_4 0.875 -0.4367463 2.186746 0.2355710
Mem_8-Mem_4 4.375  3.0632537 5.686746 0.0000001
Mem_8-Mem_6 3.500  2.1882537 4.811746 0.0000034

As you can see, it seems that memory at age eight (\(\overline{x}_{age8}=7.38\), \(SD=1.19\)) is higher than both ages four (\(\overline{x}_{age4}=3.00\), \(SD=1.07\), \(p<.001\)) and six (\(\overline{x}_{age4}=3.88\), \(SD=0.84\), \(p<.001\)). However, memory at age four did not differ than at age six (\(p=.236\)).

12.9 Effect Size

Effect sizes for repeated measures ANOVA are more difficult to calculate by hand. Specifically, we may use generalized eta squared (\(\eta_g^2\)) to account for our repeated measures.

We can get this from statistical software. For this example:

# Effect Size for ANOVA (Type I)

Group  | Parameter | Eta2 (generalized) |       95% CI
------------------------------------------------------
Within |       Age |               0.79 | [0.57, 1.00]

- Observed variables: All
- One-sided CIs: upper bound fixed at [1.00].

Thus, age appears to have a large effect on memory, \(\eta_g^2=.79\), \(95\%CI[.57, 1.00]\).

12.10 Our Results

Recall your hypothesize from above.

you hypothesize that children’s scores on the [memory] test will improve as they grow over time. (You, moments ago).

We conducted an ANOVA to test whether age has an affect on a child’s memory. We used Mauchly’s test to check the assumption of sphericity and the results indicate that the assumption is not violated, \(p = .558\). The results of our omnibus ANOVA suggest that age has a strong and statistically significant effect on a child’s memory, \(F(2, 14)=35.48\), \(\eta_g^2=.79\), \(95\%CI[.63, 1.00]\), \(p<.001\).

Post-hoc results indicated that memory at age eight (\(\overline{x}_{age8}=7.38\), \(SD=1.19\)) is higher than both ages four (\(\overline{x}_{age4}=3.00\), \(SD=1.07\), \(p<.001\)) and six (\(\overline{x}_{age4}=3.88\), \(SD=0.84\), \(p<.001\)). However, memory at age four did not differ than at age six (\(p=.236\)).

Building Your Toolbox
Name Uses Number of IVs Number of DVs IV DV Assumptions Hypotheses Effect Size
z-test Compare one group's mean to a population mean. 0 (No IVs) 1 None or Categorical (e.g., Group) Continuous Normality, known population variance Null: Mean of group equals population mean, Alternative: Mean of group differs from population mean Cohen's d
Independent t-test Compare means between two independent groups. 1 (Categorical, e.g., Group) 1 Categorical (2 groups) Continuous Normality, equal variances (for Student's t-test), independence Null: Means of the two groups are equal, Alternative: Means of the two groups differ Cohen's d (or Hedges' g)
Repeated t-test Compare means within the same group at two different times or conditions. 1 (Within-subjects, e.g., Time or Condition) 1 Within-subjects (e.g., Time or Condition) Continuous Normality, sphericity, independence Null: Mean difference between conditions is zero, Alternative: Mean difference is not zero Cohen's d or Partial Eta-squared (η²)

12.11 Repeated Measures ANOVA in R

We can use the same ez library to conduct our repeated measures ANOVA in R. Our data will need to be in long format, with each measurement having a row as opposed to each individual. The following data is in long format.

A long dataset.
ID Age Memory
1 Mem_4 3
1 Mem_6 5
1 Mem_8 7
2 Mem_4 4
2 Mem_6 3
2 Mem_8 8
3 Mem_4 3
3 Mem_6 5
3 Mem_8 5
4 Mem_4 3
4 Mem_6 3
4 Mem_8 8
5 Mem_4 4
5 Mem_6 4
5 Mem_8 7
6 Mem_4 4
6 Mem_6 4
6 Mem_8 9
7 Mem_4 1
7 Mem_6 4
7 Mem_8 7
8 Mem_4 2
8 Mem_6 3
8 Mem_8 8

As you can see, each individual has three rows, one for each time of assessment.

The ezANOVA() function will be used. It will automatically conduct Mauchly’s test because it picks up we have a ‘within’ factor:

$ANOVA
  Effect DFn DFd        F            p p<.05       ges
2    Age   2  14 35.48276 3.297595e-06     * 0.7903226

$`Mauchly's Test for Sphericity`
  Effect         W         p p<.05
2    Age 0.8235094 0.5584776      

$`Sphericity Corrections`
  Effect       GGe        p[GG] p[GG]<.05      HFe        p[HF] p[HF]<.05
2    Age 0.8499856 1.525556e-05         * 1.094312 3.297595e-06         *
Practice Question

You are a educational psychologist testing the efficacy of a new reading program for children who are at-risk for developing a reading disorder. Because assessments are time-consuming, expensive, and with a long waitlist, you are asked to implement a program ASAP and determine it’s efficacy. You develop a program based in the literature and hypothesize a significant improvement in reading ability. You measure reading ability (a measurement that uses t-scores) prior to starting the program, 1 month after being in place, 2 months after being in place (the conclusion of the program), and 3 months (one month after conclusion).

You recruit 6 individual for the program and obtain the following data:

ID T0_Month T1_Month T2_Month T3_Month
1 38 46 42 42
2 44 51 52 47
3 48 53 50 51
4 39 42 45 35
5 40 42 41 39
6 37 42 42 43 
$ANOVA
  Effect DFn DFd        F           p p<.05       ges
2   Time   3  15 6.656051 0.004470667     * 0.1668966

$`Mauchly's Test for Sphericity`
  Effect         W         p p<.05
2   Time 0.3771464 0.6150885      

$`Sphericity Corrections`
  Effect       GGe      p[GG] p[GG]<.05       HFe       p[HF] p[HF]<.05
2   Time 0.6226175 0.01702152         * 0.9798512 0.004796211         *

12.12 Additional Readings