11  One-way ANOVA

12 One-Way ANOVA

This chapter will cover the one-way ANOVA, a statistical method used to determine if there is a significant difference among the means of three or more independent groups. Unlike a t-test, which compares the means of only two groups, the one-way ANOVA extends this comparison to multiple groups to test whether at least one group mean is significantly different from the others. It calculates an F-statistic by comparing the variance between group means to the variance within groups, allowing researchers to determine whether any observed differences are statistically significant.

12.1 Some Additional Details

The one-way ANOVA is appropriate for situations where there is one independent variable (IV) with three or more levels (e.g., conditions or groups) and one continuous dependent variable (DV). For example, researchers might use a one-way ANOVA to compare test scores (DV) across three different teaching methods (IV with three levels) or to assess the effects of three different diets (IV with three levels) on weight loss (DV). Importantly, in a one-way ANOVA, the participants in each group are different.

The null hypothesis for the one-way ANOVA (herafter, I will simply write ‘ANOVA’) posits that all group means are equal:

$H_0:{\mu }_1={\mu }_2={\mu }_3=\dots ={\mu }_k$

where $k$ represents the number of groups. The alternative hypothesis states that at least one group mean is different:

$H_1:\text{At least one }{\mu }_i\text{ differs from the others.}$

This is the general structure of $H_0$ and $H_1$ in ANOVA designs.

By rejecting the null hypothesis, researchers conclude that significant differences exist among group means–a least one group differs from at least one other group. However, post hoc tests are typically required to identify where these differences occur.

12.1.1 Key Assumptions

A one-way ANOVA can be conducted under certain assumptions. These include:

12.1.1.1 1. The data are continuous

The dependent variable should be at the interval or ratio level.

12.1.1.2 2 Independence of observations

Each group should consist of independent samples. Commonly, this means that no participant appears in more than one group. This assumption is sometimes called independence of residuals.

12.1.1.3 3. Homogeneity of variances

The variance within each group should be approximately equal. This can and will be tested using Levene’s test. We want a non-statistically significant result for Levene’s test.

12.1.1.4 4. Normality

It’s a common misconception that the DV must be normally distributed. In reality, the residuals should be normally distributed. We can visualize this using a Q-Q plot or formally test this using the Shapiro-Wilks test (when sample sizes aren’t too large).

Q-Q Plot

The Q-Q plot show what a variable would like like if it were normally distributed compared with what it actually is. In essence, we order our variable and compare to what the quantiles should look like under normality. Consider the following data:

x
10.77
9.86
9.80
9.92
8.82

We could order these variables as: 8.82, 9.8, 9.86, 9.92, 10.77. Under a normal distribution, we would create five quantiles.

Believe it or not, each section in the above contains the same proportion. Thus, if data were normally distributed and we drew 5 numbers, like above, we would expect one to fall in each quantile. The QQ plot compares where we would expect values to fall on a normal curve versus where they actually are (e.g., z-score).

A Q-Q plot will look like the following:

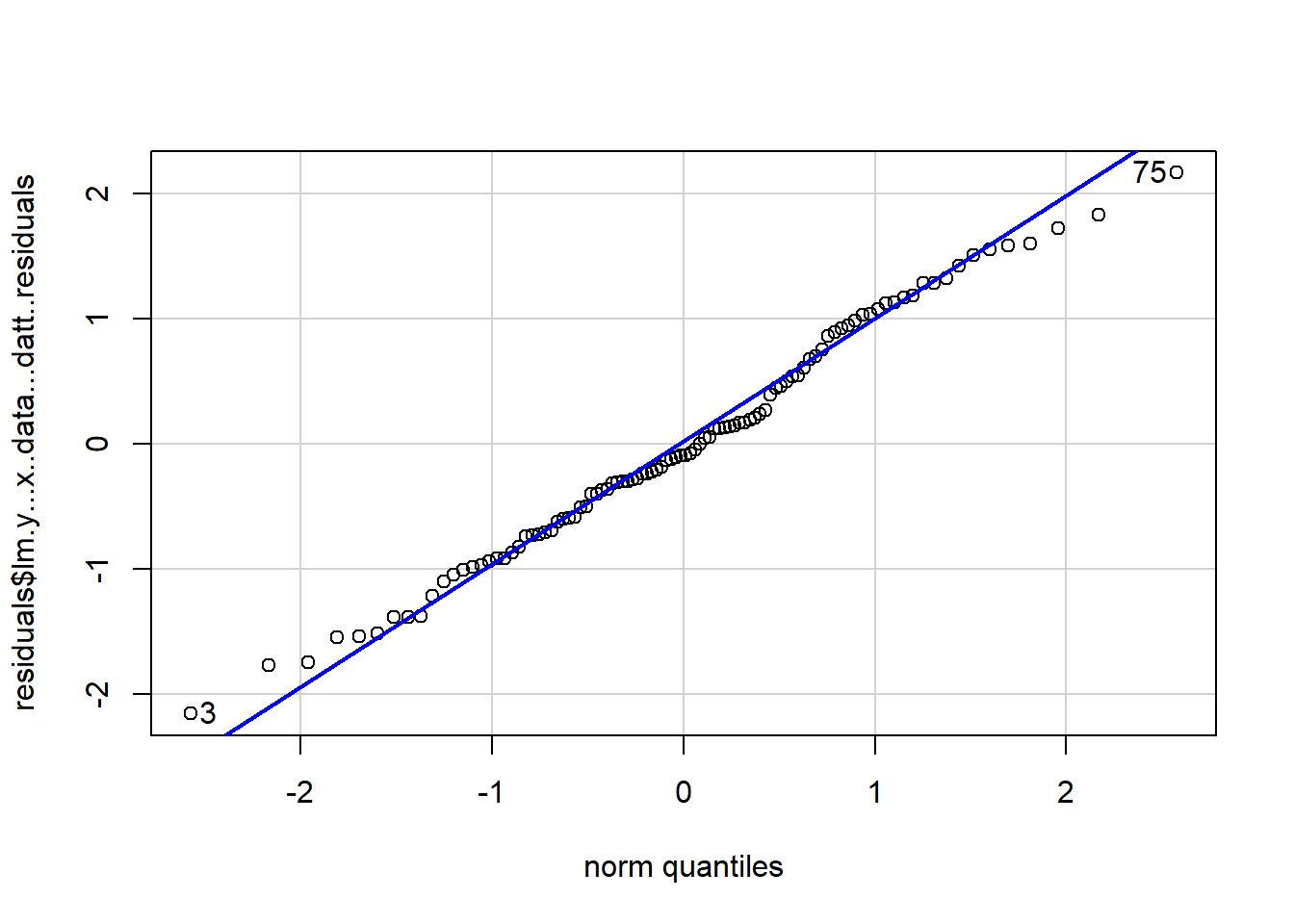
[1] 75  3

Normally distributed data will fall close to the line (vague, I know). The above graph does let us know that observation 75 appears to be particularly problematic. Typically, we would be concerned if the points systematically varied from the line.The tails typically stray farther from the line.

Shapiro-Wilks Test

The Shapiro-Wilks test assesses how far the data deviates from normality. A statistically significant result ($p<.05$) is typically interpreted as the data deviating for normality.

12.2 Treatments for OCD: What Works?

O’Connor et al. (2006) compared the efficacy of treatments for obsessive compulsive disorder (OCD). They measured the severity of OCD symptoms, with lower scores indicating better outcomes (i.e., fewer symptoms). Specifically, they compared differences in OCD severity after individuals received one of:

• Cognitive Behavioral Therapy (CBT)
• Medication
• CBT + Medication

And they believe that the CBT + Medication would show lower OCD symptoms than the other groups.

12.3 Step 1. Generate Hypotheses

The main null and alternative hypotheses for the ANOVA can be converted into a statistical hypothesis stated as (for the null):

$$H_0:{\mu }_{CBT}={\mu }_{Rx}={\mu }_{CBT+Rx}$$

And (for the alternative):

$$H_1:\text{At least one }{\mu }_i\text{ differs from the others.}$$

12.4 Step 2. Designing the Study

We will use a research design to conduct a similar analysis as O’Conner et al. using fake/hypothetical replication data. Although there are some slight adjustments, our method follows:

Participants: Participants were recruited from the Montreal community, meeting criteria for severe OCD (Y-BOCS >16). Exclusions included major psychiatric comorbidities like substance abuse or psychosis.

Materials: The Yale-Brown Obsessive Compulsive Scale (Y-BOCS) was used to assess OCD severity.

Procedure: Participants were randomly assigned to either:

1. Fluvoxamine (hereafter, Rx): for 5 months
2. CBT only: 20 sessions focusing on exposure and cognitive restructuring
3. Fluvoxamine + CBT: 20 sessions while also taking medication.

Symptoms were measured at the end of the treatment conditions. Unfortunately, we lost any pre-treatment data so we can only assess OCD severity at the end of treamtment. Thus, we have three major groups (Rx, CBT, Rx + CBT) and one outcome (OCD severity).

The ethics review board at Grenfell Campus reviewed the project and ethics submission and approved the study.

12.5 Step 3. Conducting the Study

The study was completed as described; a final sample size of 30 (10 per group) was used. The following data were obtained:

Click to expand the data

ID	Treatment	OCD_Severity
1	CBT	12
2	CBT	8
3	CBT	12
4	CBT	10
5	CBT	7
6	CBT	10
7	CBT	10
8	CBT	11
9	CBT	11
10	CBT	14
11	Rx	14
12	Rx	12
13	Rx	8
14	Rx	11
15	Rx	9
16	Rx	10
17	Rx	8
18	Rx	13
19	Rx	9
20	Rx	7
21	CBT_Rx	9
22	CBT_Rx	6
23	CBT_Rx	8
24	CBT_Rx	9
25	CBT_Rx	8
26	CBT_Rx	7
27	CBT_Rx	6
28	CBT_Rx	7
29	CBT_Rx	10
30	CBT_Rx	10

12.6 Step 4. Analyzing Data

Theoretically, we could do three t-tests:

1. CBT versus Rx
2. CBT versus CBT + Rx
3. Rx versus CBT + Rx

However, this would result in an inflated Type I error rate. Recall that we typically set our $\alpha =.05$ ($1-\alpha =.95$). With three independent comparisons our alpha rate actually becomes:

$1-(1-\alpha {)}^{n_{comparisons}}=1-(1-.05{)}^3=.142625$

Our Type I error rate would go from 5% to 14.26%! If we had four groups, we would have six possible comparisons and our Type I error rate would increase to 26.49%. The following figure represents the relationship between number of comparisons and Type I error.

Understanding this figure is important. Yes, you could do a bunch of t-tests, but you trade off your alpha rate. Instead, you could use an ANOVA.

An ANOVA allows us to compare 2+ groups within a single test – and as you will see later, multiple IVs at once. Specifically, we can test an independent variable’s (with two or more levels/groups) association with a dependent variable. Prior to diving into ANOVAs, I would like to explain the F-distribution, which is at the core of ANOVAs.

Understanding the F-Distribution (click to expand)

To understand the F-distribution, we need to explore the chi-square distribution. Imagine we measure IQ scores in a random sample of four 20-year-olds. Let’s assume IQ is normally distributed with a mean of 100 and a standard deviation of 15. For example:

Name	IQ
Alicia	85
Ramona	108
Marie	91
Julianna	108

We can standardize these scores by converting them to z-scores using the formula:

$$z=\frac{x_i-\mu }{\text{SD}}$$

Here’s how those z-scores look:

Name	IQ	z-score
Alicia	85	-1.00
Ramona	108	0.53
Marie	91	-0.60
Julianna	108	0.53

These z-scores are also called standard deviates: they represent how far each score deviates from the mean, measured in standard deviations. Since the IQ scores are independently and identically distributed (IID), we can calculate the sum of squares of these standard deviates:

$$SS=\sum _{i=1}^n{z}_i^2$$

For our sample:

$$SS=(-1{)}^2+(0.53{)}^2+(-0.6{)}^2+(0.53{)}^2=1.92$$

The chi-square value is the sum of squares of standard deviates. The chi-square distribution describes the distribution of these summed squares when sampling repeatedly (theoretically, infinitely) from a normally distributed population. For example, if we randomly sampled four IQ scores repeatedly, the sum of squared standard deviates would form a chi-square distribution with 4 degrees of freedom (df).

Here’s a plot of the chi-square distribution with 4 df:

The chi-square distribution’s shape depends only on its degrees of freedom. As the df increases, the distribution approaches a normal distribution. Here’s what the chi-square distribution looks like with various degrees of freedom:

Additionally, the chi-square distribution has a mean equal to the degrees of freedom and variance equal to two times the degrees of freedom. Thus, a chi-square distribution where $df=4$ will have a mean of 4 and variance of 8. Interesting properties!

Chi-square Shiny Application

This shiny app is made available by ‘The Art and Science of Learning from Data’.

12.6.1 Connecting Chi-Square to Variance

Recall that variance can be expressed as:

$$s^2=\frac{\sum _{i=1}^n(x_i-\overline{x}{)}^2}{n-1}$$

Interestingly, the chi-square value can be scaled to estimate variance. By dividing the sum of the standard deviates by the degrees of freedom, we approximate a variance. For our four people from the IQ example, recall that:

$$SS=(-1{)}^2+(0.53{)}^2+(-0.6{)}^2+(0.53{)}^2=1.92$$

And the approximation of a variance being:

$$\text{Scaled Chi-square}=\frac{{\chi }^2}{df}=\frac{1.92}{4-1}=0.64$$

The F-distribution is the ratio of two independent, scaled chi-square distributions. Imagine we have two chi-square distributions: one with $d{f}_1$ and the other with $d{f}_2$. The $F$-statistic is calculated as:

$$F=\frac{{\chi }_1^2/{\text{df}}_1}{{\chi }_2^2/{\text{df}}_2}$$

This ratio is central to ANOVA. In ANOVA, we compare two variances:

1. The variance of group means (MSB: mean square between).

2. The variance of individual scores within groups (MSE: mean square error).

If the groups are sampled from the same population (i.e., the null hypothesis is true), the ratio of these variances should follow the F-distribution. If group means vary substantially more than the variance within the group, than the F value should be higher. If the value is at or beyond a pre-specified value (i.e., beyond our critical alpha value), we assume that our data are unlikely given a true null hypothesis and we reject the null hypothesis.

To help you visualize the distribution, here’s an example of the $F$-distribution with $d{f}_1=4$ and $d{f}_2=36$:

You can use critical values for F-dsitribtions the same way you would for z or t tests.

12.6.2 Summary

1. The chi-square distribution describes the sum of squared standard deviates.
   
2. The F-distribution is the ratio of two independent, scaled chi-square distributions.
   
3. In ANOVA, the F-statistic tests whether the variance between group means (MSB) is significantly greater than the variance within groups (MSE).

Understanding these foundations clarifies why the F-distribution underpins ANOVA and other statistical tests comparing variances.

12.7 Step 4. Analyzing the Data (continued)

We can test these hypotheses through an ANOVA and post-hoc tests.

12.8 Our Model

Using the above hypothesis, we can frame our model as:

$outcom{e}_i=group+erro{r}_i$

or more specifically, and expanded on below:

$y_i={\beta }_0+x_{i}grou{p}_i+erro{r}_i$

12.9 Our Analysis

If you read the section about the F-statistic earlier, you’ll remember that the standard deviates (or z-scores) were squared and summed to calculate a total. We can use a similar idea when analyzing data with multiple groups.

In ANOVA, we compare two sources of variability:

1. Variability between group means: This tells us whether the group means are different from each other.

2. Variability within groups: This reflects the differences between individual scores and their group’s mean.

We calculate these as “sum of squares” values:

1. SST (Sum of Squares Total): The total variability in all the scores.
2. SSB (Sum of Squares Between Groups): The variability explained by group differences.
3. SSE (Sum of Squares Error): The variability within each group that isn’t explained by group differences.

These three components are related in a simple way:

$$SST=SSB+SSE$$

In short, the one way ANOVA breaks the total variability into two parts: what’s explained by the group differences (SSB) and what’s left over as error (SSE). By comparing these two sources of variability, we can see if the group means are significantly different from each other. Note: later we wil explore more complex types of ANOVAs that can break the total variability into more than two parts.

Descriptions of each follow along with visualizations.

12.9.1 SST

The sum of squares total represents all the deviations of the model. It is each score compared to the overall (grand) mean. Is it represented by:

$SST=\sum _{i=1}^n(x_i-\bar{x}{)}^2$

For SST, we can calculate SST by subtracting each score from the mean, squaring it, and adding up across all participants. However, there is another formula that may be easier to use:

$$SST=\sum _{i=1}^N{x}_i^2-\frac{(\sum _{i=1}^N{x}_i{)}^2}{N}$$

Here you only need three pieces of information:

1. Sum of each squared scores/value: $\sum _{i=1}^N{x}_i^2$
2. Sum of scores/values, then squared: $(\sum _{i=1}^N{x}_i{)}^2$
3. Total sample size: $N$

For our OCD data, the sum of the squared scores is 2868, the sum of the scores, then squared, is 8.1796^{4}, and N is 30. Thus, our SST is:

$$SST=\sum _{i=1}^N{x}_i^2-\frac{(\sum _{i=1}^N{x}_i{)}^2}{N}=2868-\frac{81796}{30}=141.467$$

We can also represent SST visually. This figure represents the total deviations used to calculate SST. Each dotted lined represents the difference between each individual and the grand mean (the solid black line). Remember, the grand mean is the mean of all individuals.

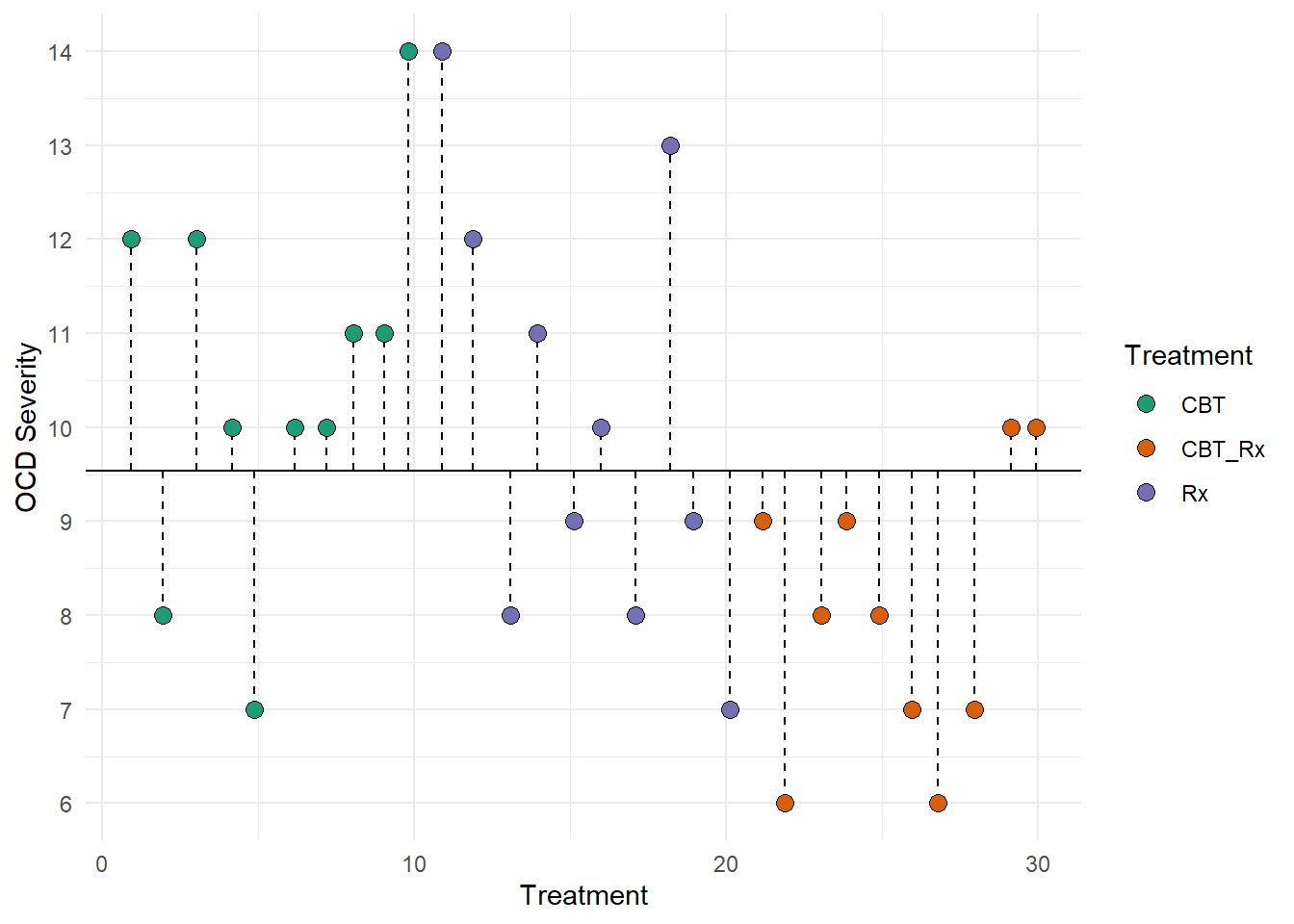
12.9.2 SSB

The sum of squares between groups (SSB) represents the deviation of each group’s mean from the grand mean.

$$SSB=\sum _{j=1}^{n_j}{n}_j({\bar{x}}_j-{\bar{x}}_{overall}{)}^2$$

where $n_j$ is the sample size for group $j$; and

${\bar{x}}_{overall}$ is the overall/grand mean.

Alternatively, the following formula may be used:

$$SSB=\sum _{i=1}^k\frac{{\left(\sum _{j=1}^{n_i}{x}_{ij}\right)}^2}{n_i}-\frac{{\left(\sum _{i=1}^k\sum _{j=1}^{n_i}{x}_{ij}\right)}^2}{N}$$

Here we need the following:

1. Sum of $x_i$, then squared for each group.
2. $n_i$ for each group.
3. Sum of $x_i$ for ALL individuals.
4. $N$, total sample size.

For us, the sum of all scores, then squared for each group are:

Treatment	Sum of Values (then squared)
CBT	11025
CBT_Rx	6400
Rx	10201

The sum of all scores (regardless of group), then squared it $81796$. Each group has $n=10$ and, thus, $N=30$.

We will calculate the first part of the formula, $\sum _{i=1}^k\frac{{\left(\sum _{j=1}^{n_i}{x}_{ij}\right)}^2}{n_i}$ for each group and then add them.

For group 1 (CBT):

$$\frac{{\left(\sum _{j=1}^{n_i}{x}_{ij}\right)}^2}{n_i}=\frac{11025}{10}=1102.5$$ For Rx:

$$\frac{{\left(\sum _{j=1}^{n_i}{x}_{ij}\right)}^2}{n_i}=\frac{10201}{10}=1020.1$$ For CBT + Rx:

$$\frac{{\left(\sum _{j=1}^{n_i}{x}_{ij}\right)}^2}{n_i}=\frac{6400}{10}=640$$

Adding these three together ive us the first part of the SSB equation:

$$\sum _{i=1}^k\frac{{\left(\sum _{j=1}^{n_i}{x}_{ij}\right)}^2}{n_i}=1102.5+1020.1+640=2762.6$$

The second part of the SSB formula is:

$$\frac{{\left(\sum _{i=1}^k\sum _{j=1}^{n_i}{x}_{ij}\right)}^2}{N}=\frac{81796}{30}=2726.533$$

And our resulting SSB:

$$SSB=2762.6-2726.533=36.067$$

It can get confusing when different places use different names for these. For example, we called the total sum of squares SST, but some places call the sum of squares between SST (treatments). Other may call the SSB, SSN (numerator). We will stick to the following for a one way ANOVA:

• Sum of squares total (SST)

• Sum of squares between groups (SSB)

• Sum of squares error (SSE)

• SST = SSB + SSE

This second figure represents SSB. Each dotted lined represents the difference between a group’s mean and the grand mean. The colored lines represent each groups mean. The black line represents the grand mean.

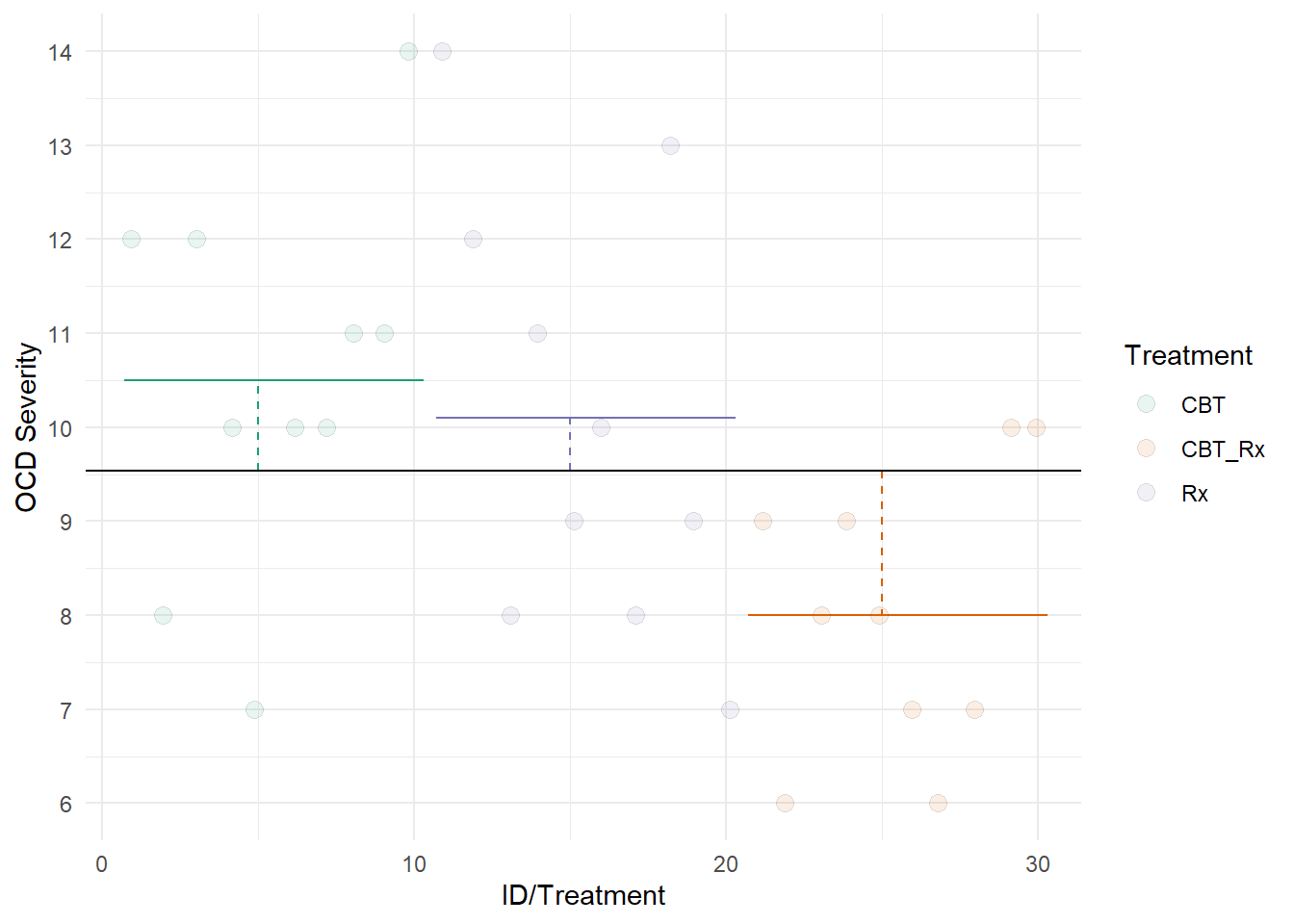
Notice that the length of the dotted lines are smaller than the lengths in the first figure. Thus, the model seems to be doing a good job at explaining our data.

12.9.3 SSE

The sum of squares error SSE represents the deviation of each individual from their group mean.

$SSE=\sum (x_{ij}-{\bar{x}}_j{)}^2$

where $x_{ij}$ is individual $i$ in group $j$ and ${\bar{x}}_j$ is the mean of group $j$. For the above data, for example the CBT group, we can calculate SSE.

An easier way to calculate this is to subtract SSB from SST. Recall the relationship between the three:

$$SST=SSB+SSE$$

and, thus:

$$SSE=SST-SSB$$

For us:

$$SSE=141.467-36.067=105.4$$

This third figure represents SSE. Each dotted lined represents the difference between an individual and their group’s mean. The colored lines represent each groups mean.

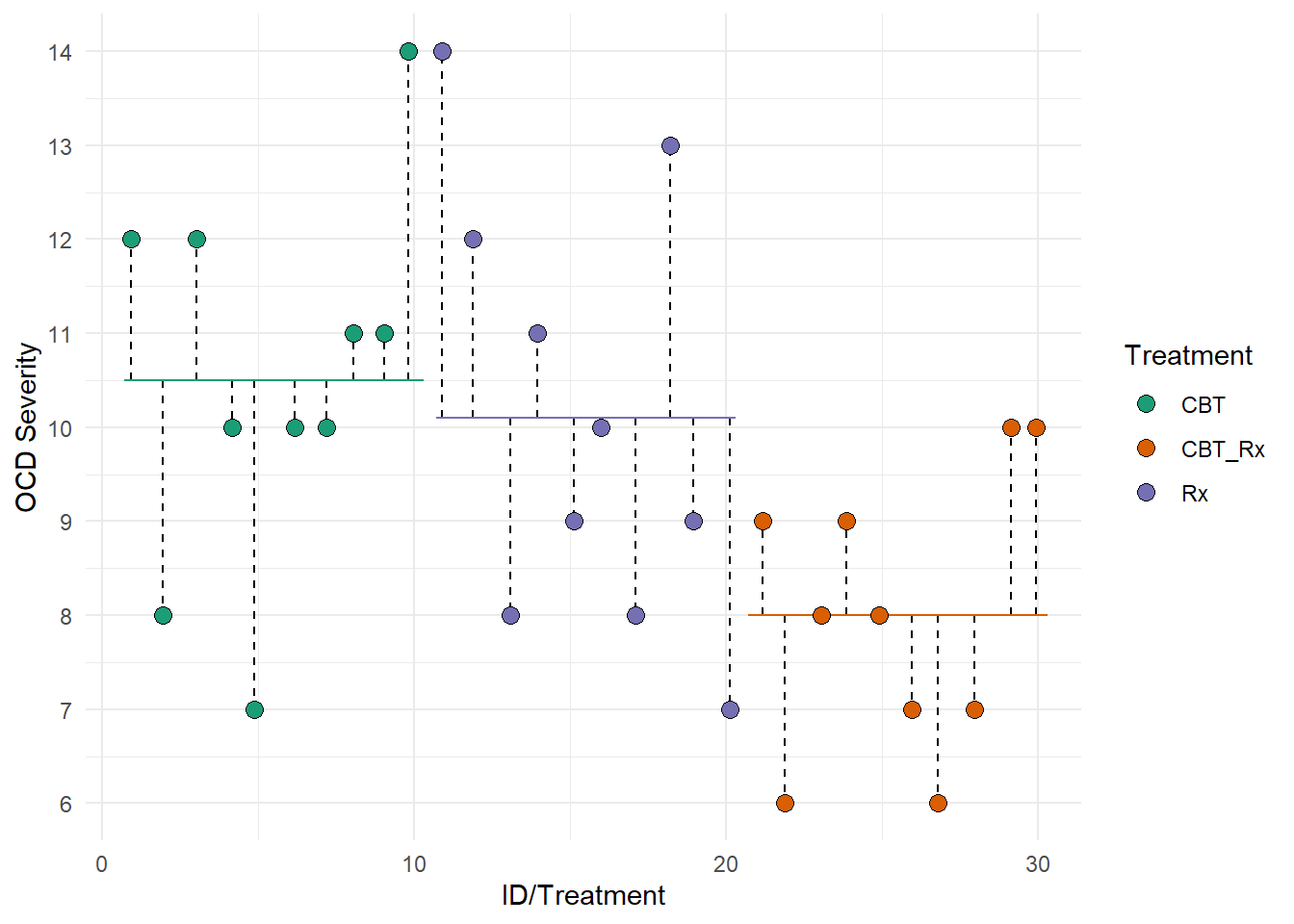
12.9.4 Mean Squares

We must also scale the sum of squares to become variances by dividing by the degrees of freedom. Our $df$ are $d{f}_b=k-1$ (where k is the number of groups) and $d{f}_e=N-k$. This results in two Mean Squares. These are, essentially, variances.

$MSB=\frac{SSB}{d{f}_b}$

and

$MSE=\frac{SSE}{d{f}_e}$

If you remember the above regarding the F distribution, you may intuitively relate it to the OCD treatment example, wherein:

$F=\frac{MSB}{MSE}$

We can determine how likely or unlikely our data are using the F-distribution of $d{f}_b$ and $d{f}_w$ degrees of freedom.

Thus, the above example would results in:

$MSB=\frac{36.06667}{3-1}=18.033$

$MSE=\frac{105.4}{30-3}=3.904$

and

$F=\frac{18.033}{3.904}=4.619$

We will compare this statistic to the distribution to determine how probable our data are compared to the null hypothesis. If our F is large enough to be unlikely given the null, we would reject it. The F statistic is an omnibus test.

Omnibus Tests

Omnibus tests, or global tests, determine the ratio of variance explained by the model versus error. In our F-test, it tells us that at least two of the means differ, but does not tell us which one. Thus, we need to conduct some form of post-hoc (after the event) tests.

If the omnibus test is not statistically significant, you can stop there. The groups in the IV do not differ.

We can use an F-distribution table to find out our approximate $p$-value. The table suggests that critical F for our degrees of freedom is $F(2,27)=2.51$ for an $\alpha =.05$. Our obtained F is higher ($F_{obtained}>F_{critical}$; $4.62>2.51$) and, thus, $p<.05$. This site can calculate exact p-values. This site returns a p-value of $p=.019$.

Our total results can be summarized in what is commonly known as an ANOVA summary table.

ANOVA Summary Table

Source	Sum of Squares	df	F Value	p-value
Between Groups	36.07	2	4.62	0.019
Within Groups	105.40	27	-	-

Any computer program you use for your analyses will provide the appropriate p-value.

Calculate p manually in R

You can use R to calculate exact p-values as well using the pf() function (probability of F). It requires arguments for your F (q), df1 and df2. Also, be sure to specify that lower.tail=F, indicating you want the probability on the right side of the distribution. For example, writing:

pf(q=4.62, df1=2, df2=27, lower.tail=F)

[1] 0.0188092

Thus, our data are quite unlikely given a true null hypothesis. We have a statistically significant result.

12.10 Post-hoc Tests

So our ANOVA revealed a statistically significant results, but it was an omnibus test. Now what? Unfortunately, the results of the omnibus ANOVA test does not inform us which groups differ. It simply tells us at least one group differ from at least one other group.

Recall that our family wise error rate increases as we do more statistical tests. So, while we may have set a criterion of $\alpha =.5$, it increases as we do more tests.

which reflect the following error rates:

Groups	Number of Possible Comparisons	Error Rate
2	1	0.050
3	3	0.143
4	6	0.265
5	10	0.401
6	15	0.537
7	21	0.659
8	28	0.762
9	36	0.842
10	45	0.901

Initially, we should test only those comparisons with which we hypothesize to be different; doing more increases the likelihood that we commit a Type 1 error. However, sometimes it makes sense to also do exploratory analyses. If we conduct exploratory analyses, we should adjust our error rate to reflect the multiple comparisons.

We will cover one major method of comparing group means: Tukey’s Honestly Significant Difference (HSD).

12.10.1 Tukey’s HSD

Tukey’s HSD provides an efficient ways to compare multiple groups simultaneously to determine if their difference is statistically significant. Basically, Tukey’s HSD provides a number with which to compare differences in group means. If two groups means’ differ by more then Tukey’s HSD, then they are statistically different.

Tukey’s HSD is, essentially, all t-test comparisons using a correction for family-wise error rates.

The formula for Tukey’s HSD is:

$T=q\times \sqrt{\frac{MSE}{n}}$

where $q$ is a critical q value, $MSE$ is the mean squared error from our ANOVA, $n$ is the sample size per group. Should the difference between the means of two groups exceed $T$, they are considered statistically different.

From our ANOVA above, we got $MSE=3.904$ and $10$ individuals per group. When we look up the critical $q$ value (for $k=3$ and $d{f}_e=27$), we get $q=3.508$. Thus, Tukey’s HSD would be:

$T=q\times \sqrt{\frac{MSE}{n}}=3.508\times \sqrt{\frac{3.904}{10}}=2.19$

Thus, we can classify any mean difference beyond 2.19 as statistically significant. Our groups are as follows:

	Mean Difference
CBT_Rx-CBT	-2.5
Rx-CBT	-0.4
Rx-CBT_Rx	2.1

However, most programs will give you specific p-values for each comparison. For example, in R:

	Mean Difference	Lower CI	Upper CI	Adjusted p-value
CBT_Rx-CBT	-2.5	-4.6908019	-0.3091981	0.0228923
Rx-CBT	-0.4	-2.5908019	1.7908019	0.8936294
Rx-CBT_Rx	2.1	-0.0908019	4.2908019	0.0621952

While our hand calculations only give us an ‘above or below’ our criteria (e.g., $p<.05$/$p>.05$), statistic programs will provide the specific p-value.

12.10.2 Bonferonni Correction

Sometimes you may wish to do some post-hoc comparisons, but without doing Tukey’s HSD. You may also apply a Bonferonni correction to the $\alpha$ level to attempt to control for the family wise error. To do so, simply use the following:

${\alpha }_{new}=\frac{\alpha }{n_{comparisons}}$

So, imagine we decide post-hoc to conduct two exploratory analyses. If our original $\alpha =.05$, then our new critical value would be: ${\alpha }_{new}=\frac{\alpha }{n_{comparisons}}=\frac{.05}{2}=.025$

12.11 Effect Size

We can calculate ${\eta }^2$ (eta squared) as an effect size for our ANOVAs. This is simply the ratio of SSB and SST. That is, deviations explained by the model over all deviations. It is an indicator for fit of our model. It ranges from 0 (nothing explained by the model) to 1 (everything explained by the model).

${\eta }^2=\frac{SSB}{SST}$

Typically, the following cut-offs are used:

• ${\eta }^2$= .01 (small effect size)
• ${\eta }^2$= .06 (medium effect size)
• ${\eta }^2$= .14 (large effect size)

Let’s calculate it for our OCD example above. We had $SSB=36.067$ and $SST=141.477$. Therefore:

${\eta }^2=\frac{36.067}{141.477}=.255$

More about the F-distribution

The following figure represents the F-distribution for $d{f}_1=2$ and $d{f}_2=27$.The red region represent the most extreme 5% of the distribution, which aligns with our pre-determine criteria of $\alpha =.05$.

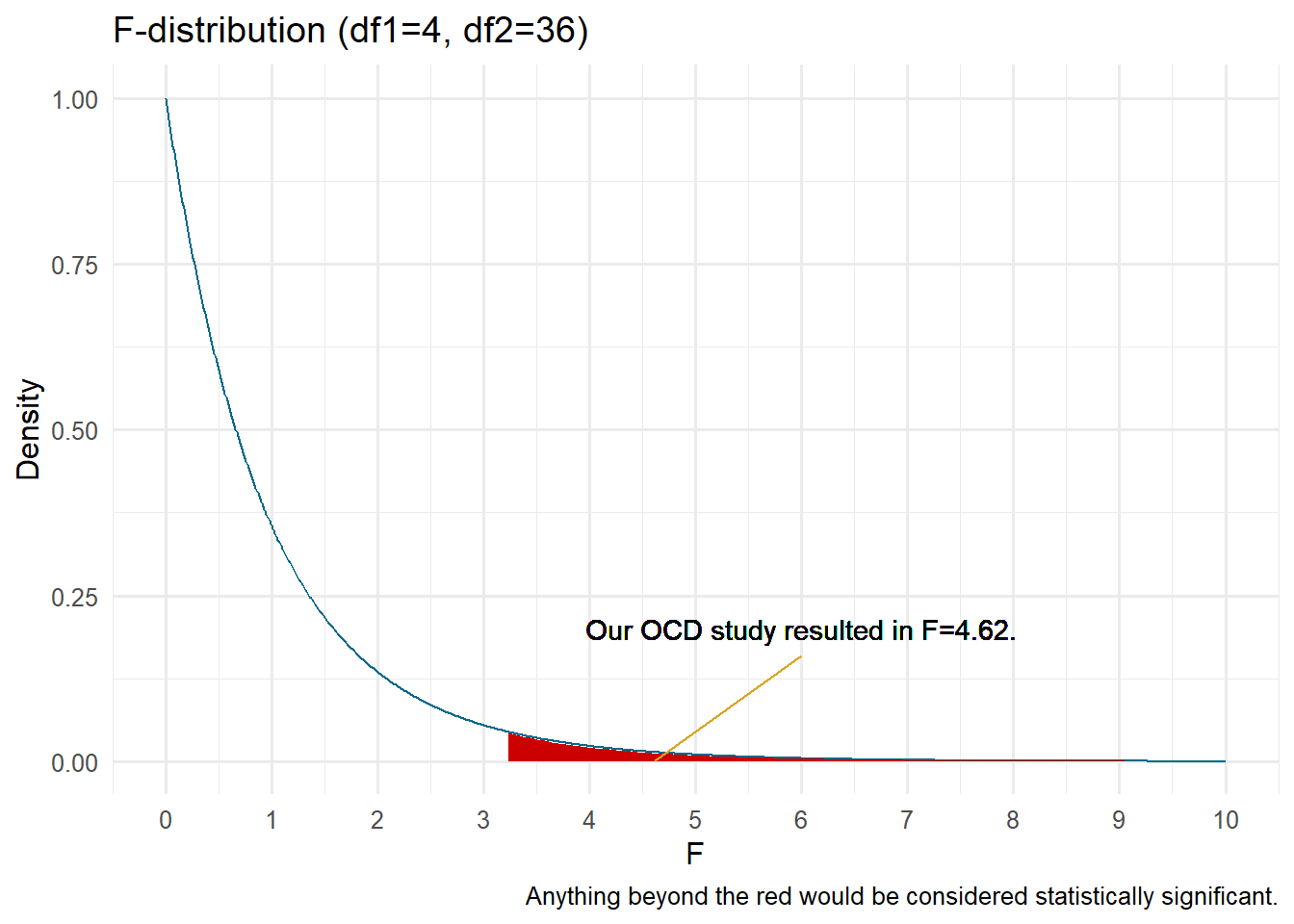
12.12 Step 5: Write up your results/conclusions

We conducted a one way ANOVA to determine the association between OCD treatments and OCD severity post-treatment. The results suggest that the group means for OCD severity are unlikely given a true null hypothesis, $F(2,27)=4.62$, $p=.019$.

Post-hoc comparisons using Tukey’s HSD were conducted to evaluate pairwise differences between the treatment groups. The results indicated a statistically significant difference between the CBT group ($\overline{x}=10.5$) and the CBT_Rx group ($\overline{x}=8.0$), $\text{mean difference}=-2.5$, $95\mathrm{\%}CI[-4.69,-0.31]$, $p_{adj}=.023$. This suggests that participants in the CBT group had significantly higher OCD severity scores compared to those in the CBT_Rx group.

No significant differences were observed between the Rx group ($\overline{x}=10.1$) and the CBT group, $\text{mean difference}=-0.4$, $95\mathrm{\%}CI[-2.59,1.79]$, $p_{adj}=.894$, or between the Rx group and the CBT_Rx group $\text{mean difference}=2.1$, $95\mathrm{\%}CI[-0.09,4.29]$, $p_{adj}=.062$.

12.13 ANOVA Model - Part 2

It may make sense to return to this section after you read the chapter on regression.

Surprisingly, you may learn that the ANOVA is the same as regression (both are general linear models). In our specific example above with three treatment groups:

$y_i={\beta }_0+x_{1i}{\beta }_1+x_{2i}{\beta }_2+e_i$

where $y_i$ is individual $i$’s score on the DV, $e_i$ is the residual/error for individual $i$, ${\beta }_n$ are regression coefficients, and $x_{ni}$ are individual $i$’s score on the $n^{th}$ variable.

What are these variables? For an ANOVA, we would use what is known as dummy coding. In dummy coding, there will be k-1 variables, where k is the number of groups. So, in the above example, we have three groups. Thus, we will have $k-1=3-1=2$ dummy variables. In dummy coding, we choose a reference category, here we can pick CBT, and the other groups are represented by the dummy variables. Thus, the CBT group will score a ‘0’ on all other $\beta$ variables. The other groups will score ‘1’ on one of the dummy variables. Importantly, each group will be the only one to score ‘1’ on the a specific dummy variable (e.g., only the Rx group scores ‘1’ on ${\beta }_1$. As a result, an individual’s score on dummy coded variables will change depending on what group that individual is in.

Additionally, most general linear models require an intercept, which is typically referred to as ${\beta }_0$. We will include an intercept that is present for ALL groups. Thus, each group would score a ‘1’ on the intercept, indicating that it is part of the linear equation for that group. The resulting table could be:

Group	CBT	Rx	CBT+Rx
${\beta }_0$	1	1	1
${\beta }_1$	0	1	0
${\beta }_2$	0	0	1

Dummy Coding

As you can see, each group has a unique pattern on the dummy variables. So how does this fit within the GLM and regression? Well, let’s focus on the placebo group. First, recall our means:

Treatment	Mean
CBT	10.5
CBT_Rx	8.0
Rx	10.1

Let’s use our brains to understand how these numbers connect to dummy coding. First, let’s consider the CBT group. Our resulting general linear model will be:

$$CBT={\beta }_0+(0){\beta }_1+(0){\beta }_2$$

therefore:

$$CBT={\beta }_0$$ because anything multiplied by 0 is 0! So this is our simplified equation for the CBT group. Our best estimate of the score of any individual in the CBT group is the mean of the CBT group. That is, if knew an individual was in CBT group and noting else about them, our best guess at their OCD severity score would be the mean of the CD severity scores of the CBT group. As a result, ${\beta }_0$ is the mean of the CBT group (here, 10.5)!

What about the Rx group?

$Rx={\beta }_0+(1){\beta }_1+0{\beta }_2$

therefore

$Rx={\beta }_0+(1){\beta }_1$

Well, we know that ${\beta }_0$ is the mean of the CBT group (10.5), and we know the mean of the Rx group (10.1). Therefore:

$Rx={\beta }_0+{\beta }_1$

$10.1=10.5+{\beta }_1$

${\beta }_1=10.1-10.5=-0.4$

Interesting. ${\beta }_1$ is simply the difference in means in CBT and Rx group, ${\beta }_1={\bar{x}}_{Rx}-{\bar{x}}_{CBT}$. I hope you can intuitively figure out what ${\beta }_2$ represents.

One important consideration here is what group we choose as the reference group (the one with “no” coefficient). This determines which means are being compared through each regression parameter, $\beta$.

Practice Question

Solve for ${\beta }_2$ in the OCD example.

Click to Reveal Answer

It is the mean difference between our reference group (CBT) and the group that is coded 1 for that variable (CBT+Rx): $2.5$.

The difference between Rx and CBT+Rx is not represented in dummy coding. We could calculate it by making either of those the refernce group.

We can also use the model to solve for an individual’s residual (error) score. Assuming we are interested in person 7 (from the CBT group; $y_7$). From the above equation, we get:

$y_7={\beta }_0+(0){\beta }_1+(0){\beta }_2+e_7$

Which simplifies to:

$y_7={\beta }_0+e_7$

because their scores are 0 on each dummy variable. Therefore, individual 7’s score is simply ${\beta }_0+e_7$. Interestingly, ${\beta }_0$ is simply the mean of the CBT group and $e_7$ is that person’s deviation from the mean of the CBT group. Here:

$10=10.5+e_7$, so

$e_7=10-10.5=-0.5$

The person’s residual score is -0.5, which is the difference between their actual score and their predicted score using our model. Remember, our best guess at their score is the mean.

Practice Question

Solve for individual $12$ in the OCD example, who is part of the Rx group and who’s OCD Severity score is 12.

Click to reveal answer

$$y_{12}={\beta }_0+(1){\beta }_1+(0){\beta }_2+e_{12}$$ Therefore:

$$y_{12}={\beta }_0+(1){\beta }_1+e_{12}$$

Filling in our beta’s from above”

$$12=10.5+(1)(-0.4)+e_{12}$$

Therefore:

$$e_{12}=12-10.5+0.4=1.9$$

When we cover regression, you will like see additional similarities in ANOVA and regression. All of the analysis we will cover are linked to the general linear model.

12.14 ANOVA in R

If you are a PSYC3950 student, you are not required to know how to calculate ANOVA in R and can skip this section. You will cover this analysis using SPSS in the lab section of the course. If you are so inclined (good for you), continue…

R can easily run the ANOVA and provide an ANOVA summary table. I particularly like the apa.aov.table() function from the apaTables library. It can quickly provide summary statistics:

library(apaTables)
#I named my data dat_ocd
one_way_anova_example <- aov(OCD_Severity~Treatment, data=dat_ocd) 
apa.1way.table(iv=Treatment, dv=OCD_Severity, data=dat_ocd)

Descriptive statistics for OCD_Severity as a function of Treatment.  

 Treatment     M   SD
       CBT 10.50 2.01
    CBT_Rx  8.00 1.49
        Rx 10.10 2.33

Note. M and SD represent mean and standard deviation, respectively.
 

and an ANOVA summary table, with effect size:

apa.aov.table(one_way_anova_example)

ANOVA results using OCD_Severity as the dependent variable
 

   Predictor      SS df      MS      F    p partial_eta2 CI_90_partial_eta2
 (Intercept) 1102.50  1 1102.50 282.42 .000                                
   Treatment   36.07  2   18.04   4.62 .019          .25         [.03, .42]
       Error  105.40 27    3.90                                            

Note: Values in square brackets indicate the bounds of the 90% confidence interval for partial eta-squared 

12.14.1 Tukey’s HSD in R

Tukey’s HSD can be found in the stats library. You simply use your ANOVA model as the main argument.

library(stats)
mod_aov <- aov(OCD_Severity ~ Treatment, data=dat_ocd)

TukeyHSD(mod_aov) #I called our ANOVA model 'mod_aov'

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = OCD_Severity ~ Treatment, data = dat_ocd)

$Treatment
           diff         lwr        upr     p adj
CBT_Rx-CBT -2.5 -4.69080194 -0.3091981 0.0228923
Rx-CBT     -0.4 -2.59080194  1.7908019 0.8936294
Rx-CBT_Rx   2.1 -0.09080194  4.2908019 0.0621952

You would interpret the last column, p adj as usual. The values have been adjusted to account for family wise error rates.

12.14.2 Assumptions

There are three assumptions within an ANOVA we must consider:

12.14.2.1 1. The residuals are normally distributed

It’s a common misconception that the DV must be normally distributed. In reality, the residuals should be normally distributed. We can visualize this using a Q-Q plot or formally test this using the Shapiro-Wilks test (when sample sizes aren’t too large).

12.14.2.1.1 Q-Q Plot

The Q-Q plot show what a variable would like like if it were normally distributed compared with what it actually is. In essence, we order our variable and compare to what the quantiles should look like under normality. Consider the following data:

x
10.77
9.86
9.80
9.92
8.82

We could order these variables as: 8.82, 9.8, 9.86, 9.92, 10.77. Under a normal distribution, we would create five quantiles.

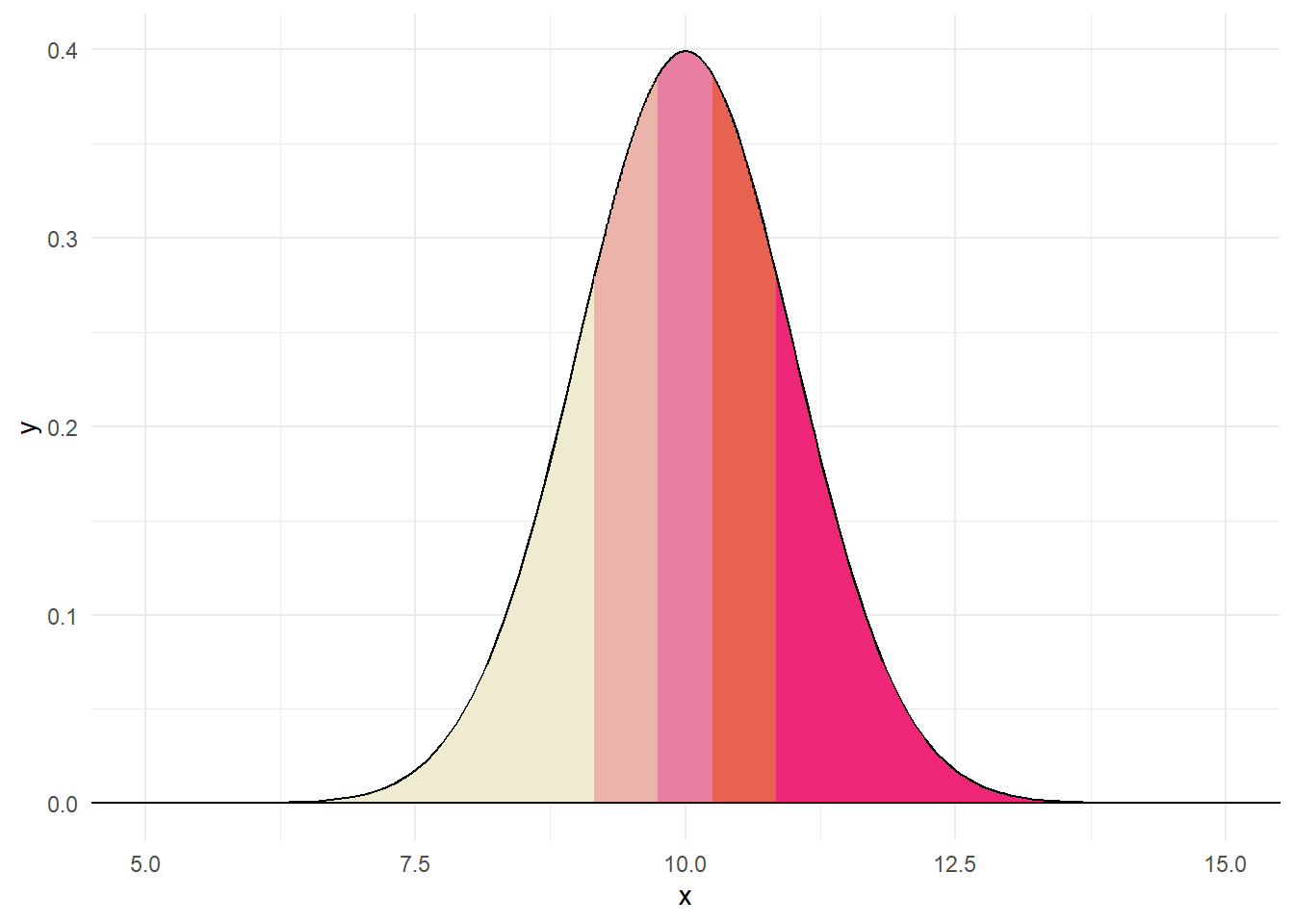
Believe it or not, each section in the above contains the same proportion. Thus, if data were normally distributed and we drew 5 numbers, like above, we would expect one to fall in each quantile. The QQ plot compares where we would expect values to fall on a normal curve versus where they actually are (e.g., z-score)

We want to conduct it on the residuals of our general model. In R:

#Setting up the model 
mod_aov <- aov(OCD_Severity ~ Treatment, data=dat_ocd)

# Getting residuals of the model
residuals <- resid(mod_aov) %>% 
  data.frame() %>% 
  rename("residual"=".")

Let’s peek at the residual for row 7 to see if it aligns with what we calculated above for the OCD example:

residuals[7,]

[1] -0.5

And we can view a Q-Q plot by using the car package:

qqPlot(residuals$residual, envelope = F)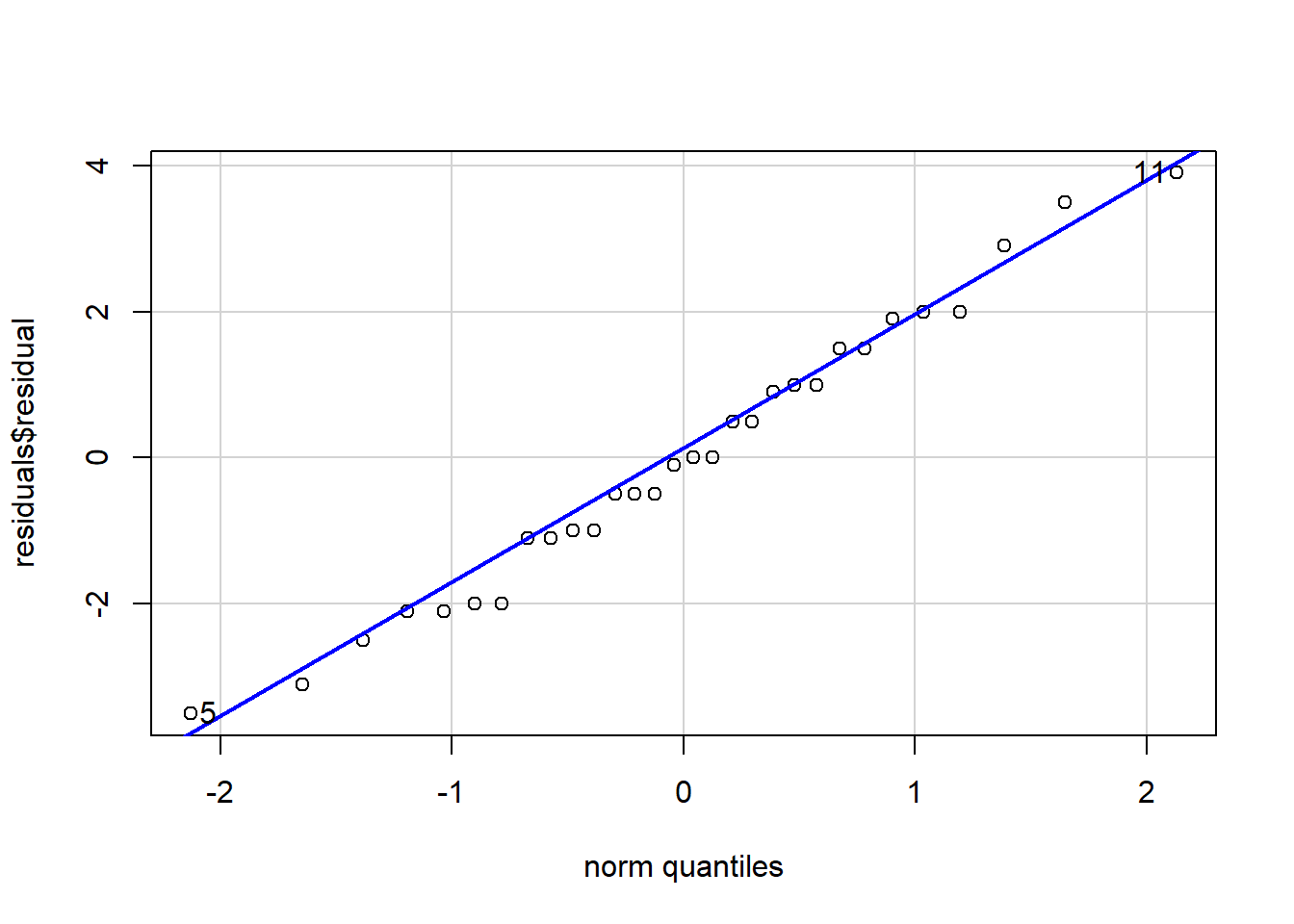

[1] 11  5

There appear to be no major deviations. Normally distributed data will fall on the line. Typically, we would be concerned if the points systematically varied from the line.

12.14.2.1.2 Shapiro-Wilks Test

The Shapiro-Wilks test assesses how far the data deviates from normality. A statistically significant result ($p<.05$) is typically interpreted as the data deviating for normality. For our residuals:

#Shapiro-Wilks
shapiro.test(residuals$residual)

    Shapiro-Wilk normality test

data:  residuals$residual
W = 0.98168, p-value = 0.8682

Thus, our data do not appear to deviate from normality.

12.14.2.2 2. Heterogeniety of Variance

Recall that the F-distribution assumes that the data come from the same population and, thus, should have the same variance. We test this using Levene’s test. Levene’s test is part of the car package which we already loaded. The arguments look similar to the ANOVA model we built:

leveneTest(OCD_Severity~Treatment, data=dat_ocd)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  2   0.925 0.4087
      27               

The results suggest that the data are likely should the groups have equal variances, $F=0.9645$, $p=.4335$. Thus, we have not violated the assumption.

12.14.2.3 3. The observations are independent

Specifically, the assumption is that the residuals are independent. That is, one residual score should not be correlated with any other residual score.

12.15 Plotting the Data

There any many ways you can visualize the results of an ANOVA. One way that is not recommended is the ‘dynamite plot’.

Dynamite plot:

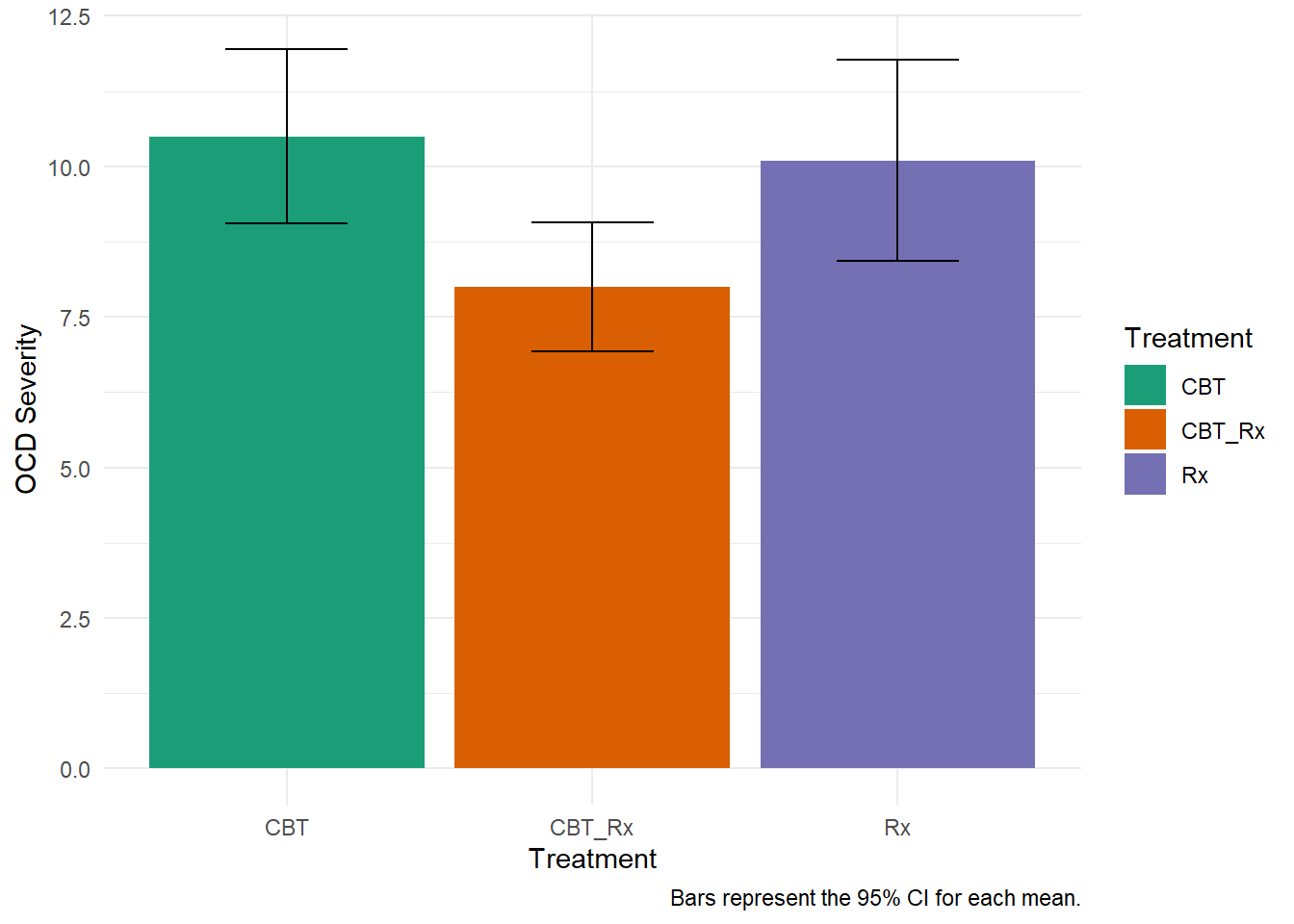
How should we visualize it? There are many ways, but one box plots may be a better method. It gives more details about the data.

Building Your Toolbox

Name	Uses	Number of IVs	Number of DVs	IV	DV	Assumptions	Hypotheses	Effect Size
z-test	Compare one group's mean to a population mean.	0 (No IVs)	1	None or Categorical (e.g., Group)	Continuous	Normality, known population variance	Null: Mean of group equals population mean, Alternative: Mean of group differs from population mean	Cohen's d
Independent t-test	Compare means between two independent groups.	1 (Categorical, e.g., Group)	1	Categorical (2 groups)	Continuous	Normality, equal variances (for Student's t-test), independence	Null: Means of the two groups are equal, Alternative: Means of the two groups differ	Cohen's d (or Hedges' g)
Repeated t-test	Compare means within the same group at two different times or conditions.	1 (Within-subjects, e.g., Time or Condition)	1	Within-subjects (e.g., Time or Condition)	Continuous	Normality, sphericity, independence	Null: Mean difference between conditions is zero, Alternative: Mean difference is not zero	Cohen's d or Partial Eta-squared (η²)
One-way ANOVA	Compare means across three or more independent groups.	1 (Categorical with 3 or more levels)	1	Categorical (3 or more groups)	Continuous	Normality, equal variances (homogeneity of variance), independence	Null: All group means are equal, Alternative: At least one group mean is different	Eta-squared (η²) or Omega-squared (ω²)

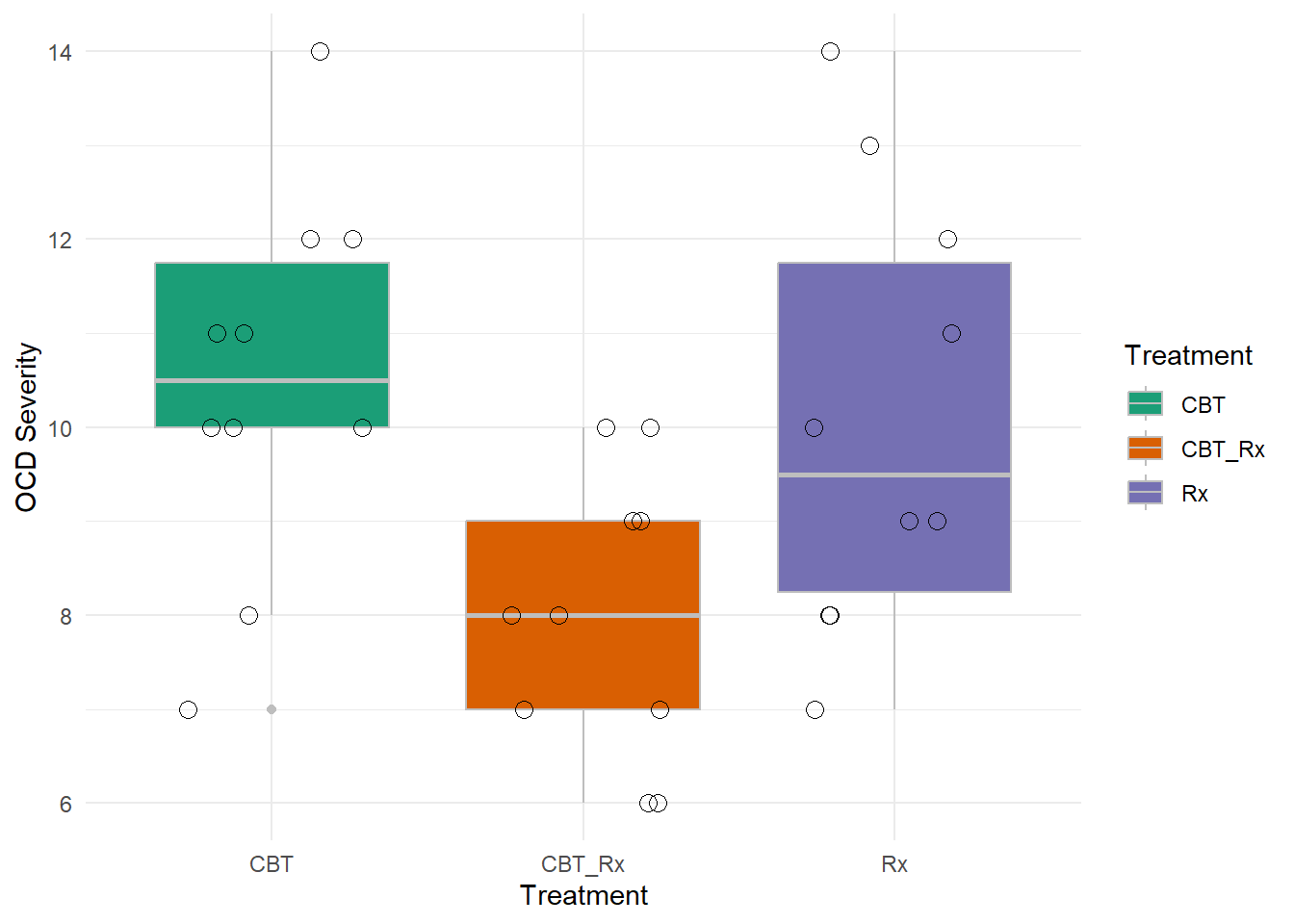
12.16 Practice Question

You are a sport psychologist testing if the type of drink improves performance. You provide three drinks to sprinters and measure the time to run 100m. The following data are obtained.

ID	Drink	Speed
1	Water	9
2	Water	15
3	Water	16
4	Water	18
5	Water	8
6	Milk	19
7	Milk	19
8	Milk	18
9	Milk	25
10	Milk	20
11	Gatorade	13
12	Gatorade	12
13	Gatorade	19
14	Gatorade	8
15	Gatorade	15

Conduct an ANOVA to determine if any groups differ from any others. Specifically:

• Write the null and alternative hypotheses

• Conduct appropriate omnibus test

• Conduct post-hoc tests.

• Calculate an effect size.

• Write a results section

Answers

Hypotheses

$H_0={\mu }_{water}={\mu }_{milk}={\mu }_{gatorade}$

$H_1=$ at least one different.

Omnibus

Means and F Table

Descriptive statistics for Speed as a function of Drink.  

    Drink     M   SD
 Gatorade 13.40 4.04
     Milk 20.20 2.77
    Water 13.20 4.44

Note. M and SD represent mean and standard deviation, respectively.
 

ANOVA results using Speed as the dependent variable
 

   Predictor     SS df     MS     F    p partial_eta2 CI_90_partial_eta2
 (Intercept) 897.80  1 897.80 61.63 .000                                
       Drink 158.80  2  79.40  5.45 .021          .48         [.05, .64]
       Error 174.80 12  14.57                                           

Note: Values in square brackets indicate the bounds of the 90% confidence interval for partial eta-squared 

Results

The ANOVA (formula: Speed ~ Drink) suggests that:

  - The main effect of Drink is statistically significant and large (F(2, 12) =
5.45, p = 0.021; Eta2 = 0.48, 95% CI [0.07, 1.00])

Effect sizes were labelled following Field's (2013) recommendations.

Tukey’s HSD

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = Speed ~ Drink, data = sprint)

$Drink
               diff         lwr        upr     p adj
Milk-Gatorade   6.8   0.3601802 13.2398198 0.0384112
Water-Gatorade -0.2  -6.6398198  6.2398198 0.9962235
Water-Milk     -7.0 -13.4398198 -0.5601802 0.0331468